


Next: 1.4.10 解答
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.8 まとめ
- 熱源として5 ℃(深層の海水の温度)、20 ℃(大気の温度)、100℃(沸騰しているお湯の温度)、1000℃(燃焼の温度)がある。この中で可逆熱機関を動作させた際に最も効率の高くなる熱源の組み合わせはどれか。また、効率を求めよ。
- 1000℃の高温熱源から900℃の低温熱源へ熱が伝わっている間で可逆熱機関を動作させた場合と、高温熱源100℃から低温熱源0℃へ熱が伝わっている間で可逆熱機関を動作させた場合を考える。どちらの場合も熱源間の温度差は100℃である。この時、それぞれの可逆熱機関の効率を求めよ。
- 300 Kの地球表面で2.7 Kの何もない宇宙空間[#!2009Fixsen!#]との間と、約6000 Kの太陽表面[#!2012Rikanenpyo!#]との間でそれぞれ可逆熱機関を動作させた際の効率を求めよ(熱源温度に地球表面温度、宇宙空間の温度、太陽の表面温度を用いる)。
- 式(1.17)
 と式(1.37)
と式(1.37)
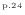 より温度
より温度
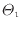 [K]の熱源と温度
[K]の熱源と温度
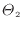 [K]の熱源(
[K]の熱源(
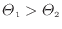 )で動作する可逆ヒートポンプの効率を示せ。
)で動作する可逆ヒートポンプの効率を示せ。



Next: 1.4.10 解答
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.8 まとめ
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camellia.thyme.jpで公開している。