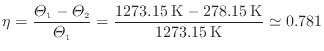
効率は0.781である。
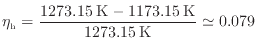
100℃と0℃の組合せでの効率
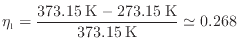
このように同じ温度差で可逆熱機関を動作させた場合でも、熱源の温度によって効率は大きく異なる。 900℃の低温熱源で効率0.268を得るには1130.14℃の高温熱源が必要である。
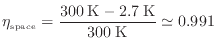
太陽との組合せでの効率
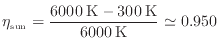
このように宇宙空間と地球表面での方が効率が高いが、伝わる熱量は太陽からの方が圧倒的に大きいため、動作させれば得られる仕事は太陽との方が大きくなる。
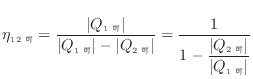
ここに式(1.37)
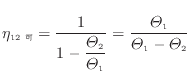
可逆ヒートポンプの効率は熱源の温度により上式のように表される。