A 熱力学第一法則とエネルギーの付録 A 熱力学第一法則とエネルギーの付録 A.2 位置エネルギー

A.1 仕事が状態量ではないのは何故か

仕事が状態量ではないのは何故かを数学的に説明した後、変化の例を示す。

A.1.1 仕事の関数

仕事の関数を仮定し、それが成り立たないことから、仕事が状態量ではないことを説明していく。系が受け取る仕事を正とすれば、仕事 $W$ [J] は一定の圧力 $P_{\mathrm{一定}}$ [Pa] の下で体積 $V$ [m³] により次式で表すことができる。

\displaystyle W=-P_{一定}\Delta V

(A.1)

このように仕事は二つの状態量である圧力と体積から求められる。しかし、仕事は一つの組み合わせの圧力と体積に対して一つの値をもつ状態量ではない。

式(A.1)から何故仕事が状態量にならないのかを考える。仕事は、ある状態１から異なる状態２へ変化した際に作用するエネルギーである。この仕事が状態量であれば、状態１、状態２ともに値を持つということなので、状態が変化した際の値は内部エネルギーのように変化量として表されることになる。そこで、仕事と同じ式(A.1)で変化量を表すことの出来る、 $P$ と $V$ の関数である状態量の仕事エネルギー $L(P,V)$ [J] が存在すると仮定する。

\displaystyle\Delta L=-P_{\mathrm{一定}}\Delta V

(A.2)

仕事エネルギーの関数 $L(P,V)$ が存在すれば、ある特定の状態 $(P,V)$ に対して一つだけの仕事 $L$ の値が決まり、仕事は状態量といえる。関数が存在することを示すためには交換法則が成り立つことを示せばよい。二階偏微分可能で連続な $C^{2}$ 級の関数は二階偏微分において必ず次式の交換法則が成り立つ¹¹1詳細は微分積分の教科書[15][27][16]を参照するとよい。。

\displaystyle\underbrace{\dfrac{\partial}{\partial V}\dfrac{\partial L}{% \partial P}=\dfrac{\partial}{\partial P}\dfrac{\partial L}{\partial V}}_{L(P,V% )が存在するための条件}

(A.3)

この交換法則が成り立たない場合には、仮定した仕事エネルギーの関数 $L(P,V)$ は存在しないといえる。

関数 $L(P,V)$ では交換法則が成り立たないことから、仕事エネルギー $L(P,V)$ は関数でないことを示し、仕事は状態量であるという仮定は間違っていることを示す。 $L(P,V)$ の微小変化を式(A.2)から求め、全微分の形に変形する。

	$\displaystyle\mathrm{d}L$	$\displaystyle=-P\mathrm{d}V$
	$\displaystyle\mathrm{d}L$	$\displaystyle=0\mathrm{d}P-P\mathrm{d}V$		(A.4)

全微分の定義から次式を得る。

\displaystyle\mathrm{d}L=\dfrac{\partial L}{\partial P}\mathrm{d}P+\dfrac{% \partial L}{\partial V}\mathrm{d}V

(A.5)

式(A.4)と式(A.5)の対応から次の二式が求まる。

	$\displaystyle\dfrac{\partial L}{\partial P}$	$\displaystyle=0$		(A.6)
	$\displaystyle\dfrac{\partial L}{\partial V}$	$\displaystyle=-P$		(A.7)

上二式左辺の一階偏微分は、さらに一階偏微分可能で連続であることは明らかである²²20は $P$ 、 $V$ どちらで偏微分しても0であり偏微分可能である。 $P$ は $P$ で偏微分すれば1、 $V$ で偏微分すれば0である。ので元の仮定した関数 $L(P,V)$ は二階偏微分可能で連続な $C^{2}$ 級の関数である。

式(A.6)と式(A.7)をそれぞれ $V$ と $P$ で偏微分し、式(A.3)が成り立つかを確認する。式(A.6)を $V$ で偏微分する。

\displaystyle\dfrac{\partial}{\partial V}\dfrac{\partial L}{\partial P}=0

(A.8)

次に式(A.7)を $P$ で偏微分する。

\displaystyle\dfrac{\partial}{\partial P}\dfrac{\partial L}{\partial V}=-1

(A.9)

式(A.8)と式(A.9)より式(A.3)が明らかに成り立たないことから、関数 $L(P,V)$ は存在しないことが分かる。よって状態量となる仕事の関数 $L(P,V)$ は存在せず、仕事は状態量ではない。

仕事を表す式(A.4)の様に積分して関数が得られない（状態量にならない）微分方程式を不完全微分方程式（Inexact differential equation）と呼ぶ。この不完全微分方程式を積分する際には、 $P$ と $V$ の積分範囲を指定するだけでは積分値を求められず、積分経路を指定した経路積分をしなくてはならない。これに対して、二階偏微分の交換法則がなりたてば、積分後の関数が存在する。そのような（状態量となる）微分方程式を完全微分方程式（Exact differential equation）と呼ぶ。

経路積分の必要な不完全微分方程式を完全微分方程式と区別するため $\mathrm{d}$ ではなく $\delta$ を使って表す。微小量の仕事は次のように表される。

\displaystyle\delta W=-P\mathrm{d}V

(A.10)

仕事や熱の特徴として、内部エネルギーなどが変化量 $\Delta U$ の微小量として $\mathrm{d}U$ が使われていることに対して、仕事や熱の $\delta W$ や $\delta Q$ は不完全微分方程式であることに加え、微小な変化量ではなく、状態変化の間に作用している仕事や熱の微小な大きさを表していることを注意して欲しい。

A.1.2 具体的な例

具体的な例で仕事が状態量とならないことを示す。ある閉じた系の体積が3.0 $\times$ 10^-3 m³（3.0 リットル）、圧力が1.0 $\times$ 10⁵ Pa（おおよそ大気圧）である状態1から、体積1.0 $\times$ 10^-3 m³（1.0 リットル）、圧力3.0 $\times$ 10⁵ Paの状態2まで変化させた際の異なる経路での系がされる仕事を計算していく。図A.1に経路ごとの圧力 $P$ 、体積 $V$ 、仕事 $W$ の関係をグラフに示す。

Figure A.1: 経路による仕事の変化

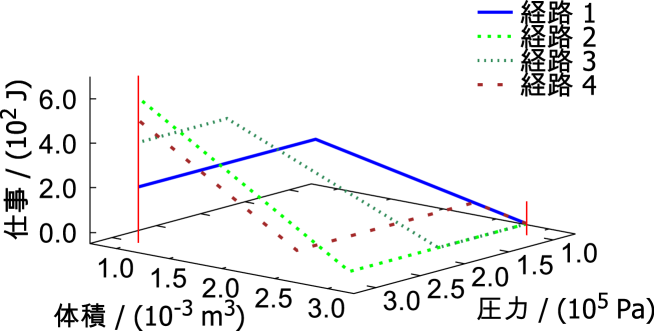
経路1

体積1.0 $\times$ 10^-3 m³まで圧力1.0 $\times$ 10⁵ Paで等圧変化

（仕事： $W=-P\Delta V=-1.0\times 10^{5}\;\mathrm{Pa}\times(1.0\times 10^{-3}\;\mathrm{m% ^{3}}-3.0\times 10^{-3}\;\mathrm{m^{3}})=2.0\times 10^{2}\;\mathrm{J}$ ）

その後、圧力3.0 $\times$ 10⁵ Paまで等積変化

（仕事は体積変化がないので $W=0$ J）

合計の仕事

2.0 $\times 10^{2}$ J + 0 J = 2.0 $\times 10^{2}$ J

経路2

圧力3.0 $\times$ 10⁵ Paまで等積変化

（仕事は体積変化がないので $W=0$ J）

その後、体積1.0 $\times$ 10^-3 m³まで等圧変化

（仕事： $W=-P\Delta V=-3.0\times 10^{5}\;\mathrm{Pa}\times(1.0\times 10^{-3}\;\mathrm{m% ^{3}}-3.0\times 10^{-3}\;\mathrm{m^{3}})=6.0\times 10^{2}\;\mathrm{J}$ ）

合計の仕事

0 J + 6.0 $\times 10^{2}$ J = 6.0 $\times 10^{2}$ J

経路3

圧力2.0 $\times$ 10⁵ Paまで等積変化

（仕事は体積変化がないので $W=0$ J）

その後、体積1.0 m³まで等圧変化

（仕事： $W=-P\Delta V=-2.0\times 10^{5}\;\mathrm{Pa}\times(1.0\times 10^{-3}\;\mathrm{m% ^{3}}-3.0\times 10^{-3}\;\mathrm{m^{3}})=4.0\times 10^{2}\;\mathrm{J}$ ）

さらに、圧力3.0 $\times$ 10⁵ Paまで等積変化

（仕事は体積変化がないので $W=0$ J）

合計の仕事

0 J + 4.0 $\times 10^{2}$ J + 0 J = 4.0 $\times 10^{2}$ J

経路4

体積2.5 $\times$ 10^-3 m³まで圧力1.0 $\times$ 10⁵ Paで等圧変化

（仕事： $W=-P\Delta V=-1.0\times 10^{5}\;\mathrm{Pa}\times(2.5\times 10^{-3}\;\mathrm{m% ^{3}}-1.0\times 10^{-3}\;\mathrm{m^{3}})=0.5\times 10^{2}\;\mathrm{J}$ ）

その後、圧力3.0 $\times$ 10⁵ Paまで等積変化

（仕事は体積変化がないので $W=0$ J）

さらに、体積1.0 $\times$ 10^-3 m³まで圧力3.0 $\times$ 10⁵ Paで等圧変化

（仕事： $W-P\Delta V=-3.0\times 10^{5}\;\mathrm{Pa}\times(1.0\times 10^{-3}\;\mathrm{m^% {3}}-2.5\times 10^{-3}\;\mathrm{m^{3}})=4.5\times 10^{2}\;\mathrm{J}$ ）

合計の仕事

0.5 $\times 10^{2}$ J + 0 J + 4.5 $\times 10^{2}$ J = 5.0 $\times 10^{2}$ J

このように状態1（圧力 1.0 $\times$ 10⁵ Pa、体積 3.0 $\times$ 10^-3 m³）から状態2（圧力 3.0 $\times$ 10⁵ Pa、体積 1.0 $\times$ 10^-3 m³）への変化において経路が異なれば仕事が異なる。状態量は状態によってのみ決まる量であるので、仕事が状態量であればどの経路でも終わりの状態で同じ値となり、同じ一つの面上に含まれる線で変化しなくてはならない。

A.1.3 経路積分

経路積分により、前節のように単純な過程の組み合わせでない経路の積分を経路全体で行い仕事を求める。経路積分では媒介変数が用いられ経路が指定される。媒介変数として時間 $t$ [s] を取り具体的な計算をしてみる。

時間0 sでの体積 $V_{0}$ = 3.0 $\times$ 10^-3 m³（3.0 リットル）、圧力 $P_{0}$ = 1.0 $\times$ 10⁵ Pa（約一気圧）からの変化を計算する。体積 $V$ は次式のように初め $V_{0}$ = 3.0 $\times$ 10^-3 m³（3.0 リットル）から1 s毎に0.1 $\times$ 10^-3 m³圧縮されるとする。

\displaystyle V

\displaystyle=3\times 10^{-3}\;\mathrm{m^{3}}-0.1\times 10^{-3}\;\mathrm{m^{3}% }\times t/\mathrm{s}

(A.11)

圧力 $P$ 変化には二原子分子の理想気体が可逆断熱変化したと仮定し、「 $PV^{1.4}=$ 一定」の関係を用いる。

$\displaystyle PV^{1.4}$	$\displaystyle=P_{0}V_{0}^{1.4}$
$\displaystyle P$	$\displaystyle=\frac{P_{0}V_{0}^{1.4}}{V^{1.4}}$
	$P_{0}$ 、 $V_{0}$ の値と式(A.11)の $V$ を代入する
	$\displaystyle=\frac{1\times 10^{5}\;\mathrm{Pa}\times(3\times 10^{-3}\;\mathrm% {m^{3}})^{1.4}}{(-0.1\times 10^{-3}\;\mathrm{m^{3}}\times t/\mathrm{s}+3\times 1% 0^{-3}\;\mathrm{m^{3}})^{1.4}}$
	$\displaystyle=\frac{1\times 10^{5}\;\mathrm{Pa}\times 3^{1.4}\times 10^{-3% \times 1.4}\;\mathrm{m}^{3\times 1.4}}{(-0.1\;t/\mathrm{s}+3)^{1.4}\times 10^{% -3\times 1.4}\;\mathrm{m}^{3\times 1.4}}$
	$\displaystyle=\left(\frac{3}{-0.1\;t/\mathrm{s}+3}\right)^{1.4}\times 10^{5}\;% \mathrm{Pa}$
	$\displaystyle=\left(\frac{1}{-\dfrac{t/\mathrm{s}}{30}+1}\right)^{1.4}\times 1% 0^{5}\;\mathrm{Pa}$
	$\displaystyle=\left(-\dfrac{t/\mathrm{s}}{30}+1\right)^{-1.4}\times 10^{5}\;% \mathrm{Pa}$	(A.12)

式(A.11)に示すように $V$ は $t$ のみの一変数関数として表されている。 $V$ の $t$ での微分を求める。

	$\displaystyle\dfrac{\mathrm{d}V}{\mathrm{d}t}$	$\displaystyle=-0.1\times 10^{-3}\;\mathrm{m^{3}/s}$
	$\displaystyle\mathrm{d}V$	$\displaystyle=-0.1\times 10^{-3}\;\mathrm{m^{3}/s}\;\mathrm{d}t$		(A.13)

仕事の微小量を求める式(A.10)に式(A.12)と式(A.13)を代入して0 sから $t_{\mathrm{f}}$ まで経路積分をする。経路中にされた仕事を求めたいので、0 sでの仕事は0 Jである。

	$\displaystyle\int^{t=t_{\mathrm{f}}}_{t=0}\delta W$	$\displaystyle=\int^{t=t_{\mathrm{f}}}_{t=0}-P\mathrm{d}V$
		$\displaystyle=\int^{t_{\mathrm{f}}}_{0}-\left\{\left(-\dfrac{t/\mathrm{s}}{30}% +1\right)^{-1.4}\times 10^{5}\;\mathrm{Pa}\right\}(-0.1\times 10^{-3}\;\mathrm% {m^{3}/s}\;\mathrm{d}t)$
		$\displaystyle=\int^{t_{\mathrm{f}}}_{0}\left\{\left(-\dfrac{t/\mathrm{s}}{30}+% 1\right)^{-1.4}\times 10\;\mathrm{Pa}\;\mathrm{m^{3}/s}\right\}\mathrm{d}t$
		$\displaystyle=\int^{t_{\mathrm{f}}}_{0}\left\{\left(-\dfrac{t/\mathrm{s}}{30}+% 1\right)^{-1.4}\times 10\;\mathrm{J/s}\right\}\mathrm{d}t$
		$\displaystyle=\left[\frac{1}{\{-1/(30\;\mathrm{s})\}(-0.4)}\left(-\dfrac{t/% \mathrm{s}}{30}+1\right)^{-0.4}\times 10\;\mathrm{J/s}\right]^{t_{\mathrm{f}}}% _{0}$
		$\displaystyle=\left[\left(-\dfrac{t/\mathrm{s}}{30}+1\right)^{-0.4}\right]^{t_% {\mathrm{f}}}_{0}\times\frac{30\;\mathrm{s}\times 10}{0.4}\;\mathrm{J/s}$
		$\displaystyle=\left\{\left(-\dfrac{t_{\mathrm{f}}/\mathrm{s}}{30}+1\right)^{-0% .4}-\left(-\dfrac{0/\mathrm{s}}{30}+1\right)^{-0.4}\right\}\times 750\;\mathrm% {J}$
		$\displaystyle=\left\{\left(-\dfrac{t_{\mathrm{f}}/\mathrm{s}}{30}+1\right)^{-0% .4}-1\right\}\times 750\;\mathrm{J}$

この変化を前節と同じように図A.2に表す。状態の変化に対して仕事が線で表される。

Figure A.2: 媒介変数表示による仕事

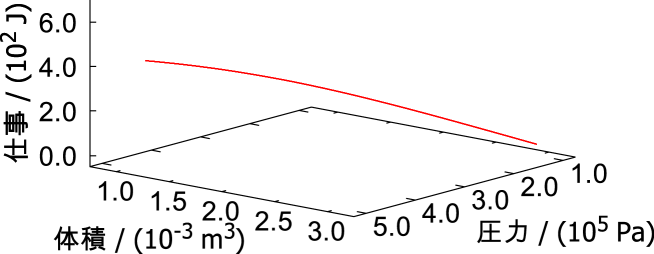
A.1.4 熱も状態量ではない

熱も状態量ではないことを示す。熱は熱力学の第一法則に示されるように状態量である内部エネルギーの差から状態量でない仕事を引いた値であるから、仕事と同様に状態量ではない³³3もし熱が状態量であれば、状態量である内部エネルギーから状態量であるとする熱の差で求められる仕事も状態量でなくてはならない。仕事は状態量ではないので、熱も状態量ではあり得ない。。仕事が状態量であるとサイクルで元の状態に戻ると差が0とならなくてはならない。周囲にした仕事と、周囲からされた仕事が等しいと言うことなので正味の仕事は0 Jとなり、正味の仕事を取り出す熱機関のサイクルをつくることは出来ないことになる。現実には仕事は状態量ではないので、熱機関となるサイクルが存在している。

A 熱力学第一法則とエネルギーの付録 References A.2 位置エネルギー

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。