C 熱力学第零法則と温度の付録 C.1 温度の測定 D 閉じた系のサイクルの付録

C.2 理想気体温度と熱力学的絶対温度

理想気体温度と熱力学的絶対温度について、双方において可逆サイクルにおける熱の比と理想気体温度の比が等しくなることを示す。

理想気体の状態方程式は次のように表される。

\displaystyle PV=nk_{\mathrm{B}}N_{\mathrm{A}}\varTheta

(C.1)

ここで、アボガドロ数 $N_{\mathrm{A}}=6.022\;140\;76\times 10^{23}\;\mathrm{mol}^{-1}$ 、ボルツマン定数 $k_{\mathrm{B}}=1.380\;649\times 10^{-23}\;\mathrm{J/K}$ 。ボルツマン定数 $k_{\mathrm{B}}$ とアボガドロ数 $N_{\mathrm{A}}$ の積は気体定数となる。

\displaystyle PV=nR\varTheta_{\mathrm{ideal}}

(C.2)

可逆サイクルである理想気体で構成されるカルノーサイクルを考え、温度と熱源とやりとりする熱との関係を示す。

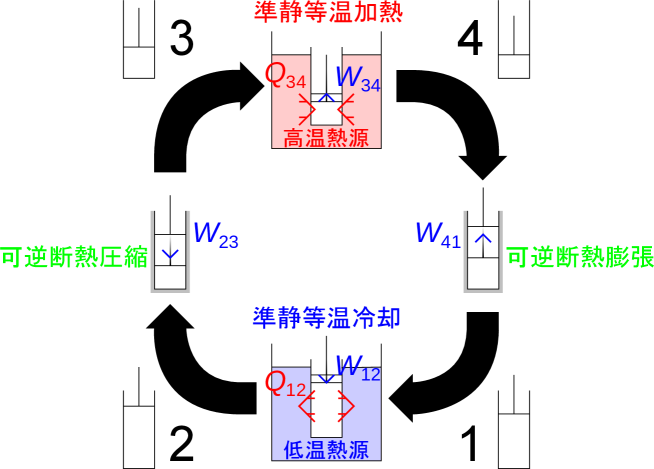
Figure C.4: 可逆サイクル（カルノーサイクル）

C.2.1 準静等温過程での関係

準静等温過程での関係を示すことで、熱源とのやりとりがわかる。カルノーサイクルは準静等温過程と可逆断熱過程の組み合わせであり、熱源との熱のやりとりは準静等温過程でのみ行われる。

高温側の準静等温膨張過程（3→4）と低温側の準静等温圧縮過程（1→2）でのエネルギーの保存式はそれぞれ次のように表される。

	$\displaystyle U_{4}-U_{3}$	$\displaystyle=W_{34}+Q_{34}$
	$\displaystyle U_{2}-U_{1}$	$\displaystyle=W_{12}+Q_{12}$

理想気体の内部エネルギーは温度のみの関数であるので、等温過程では変化しない。よって上式はそれぞれ次のように表される。

	$\displaystyle Q_{34}$	$\displaystyle=-W_{34}$		(C.3)
	$\displaystyle Q_{12}$	$\displaystyle=-W_{12}$

上式で示されるように、仕事を求めれば熱源と交換される熱の大きさが分かるため、準静等温過程における仕事を求める。

	$\displaystyle W_{34}$	$\displaystyle=\int^{V_{4}}_{V_{3}}P\mathrm{d}V$
		$\displaystyle=\int^{V_{4}}_{V_{3}}\frac{nR\varTheta_{\mathrm{ideal,34}}}{V}% \mathrm{d}V$
		$\displaystyle=nR\varTheta_{\mathrm{ideal,34}}\int^{V_{4}}_{V_{3}}\frac{1}{V}% \mathrm{d}V$
		$\displaystyle=nR\varTheta_{\mathrm{ideal,34}}\left[\log_{e}V\right]^{V_{4}}_{V% _{3}}$
		$\displaystyle=nR\varTheta_{\mathrm{ideal,34}}(\log_{e}V_{4}-\log_{e}V_{3})$
		$\displaystyle=nR\varTheta_{\mathrm{ideal,34}}\log_{e}\frac{V_{4}}{V_{3}}$

上式と式(C.3)より次の式が求められる。

\displaystyle Q_{34}

\displaystyle=-nR\varTheta_{\mathrm{ideal,34}}\log_{e}\frac{V_{4}}{V_{3}}

(C.4)

同様に低温側の準静等温圧縮過程（1→2）についても計算すると次式を得る。

\displaystyle Q_{12}

\displaystyle=-nR\varTheta_{\mathrm{ideal,12}}\log_{e}\frac{V_{2}}{V_{1}}

(C.5)

C.2.2 可逆断熱過程での関係

可逆断熱過程での関係を求める。まず、理想気体の内部エネルギーの変化が等積比熱により求められることを示す。

内部エネルギーを温度 $\varTheta_{\mathrm{ideal}}$ と体積 $V$ の関数として $U(\varTheta_{\mathrm{ideal}},V)$ として表すと、他変数関数の微分の定義より次式が得られる。

	$\displaystyle\mathrm{d}U$	$\displaystyle=\bigg{(}\dfrac{\partial U}{\partial\varTheta_{\mathrm{ideal}}}% \bigg{)}_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}+\bigg{(}\dfrac{\partial U}{% \partial V}\bigg{)}_{\varTheta_{\mathrm{ideal}}}\mathrm{d}V$
理想気体では内部エネルギーは温度のみの関数であるので
		$\displaystyle=\bigg{(}\dfrac{\partial U}{\partial\varTheta_{\mathrm{ideal}}}% \bigg{)}_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}$
定積熱容量の定義から $C_{V}=\bigg{(}\dfrac{\partial U}{\partial\varTheta_{\mathrm{ideal}}}\bigg{)}_{V}$
		$\displaystyle=C_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}$	(C.6)

次に断熱過程においてサイクルの内部エネルギーは仕事によってのみ変化するため、次式が成り立つ。

	$\displaystyle\mathrm{d}U$	$\displaystyle=-P\mathrm{d}V$
式(C.6)より
	$\displaystyle C_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}$	$\displaystyle=-P\mathrm{d}V$
	$\displaystyle C_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}+P\mathrm{d}V$	$\displaystyle=0$
理想気体の状態方程式より $P=\dfrac{nR\varTheta_{\mathrm{ideal}}}{V}$
	$\displaystyle C_{V}\mathrm{d}\varTheta_{\mathrm{ideal}}+\frac{nR\varTheta_{% \mathrm{ideal}}}{V}\mathrm{d}V$	$\displaystyle=0$
	$\displaystyle\frac{1}{\varTheta_{\mathrm{ideal}}}\mathrm{d}\varTheta_{\mathrm{% ideal}}+\frac{nR}{C_{V}}\frac{1}{V}\mathrm{d}V$	$\displaystyle=0$
	$\displaystyle\int\frac{1}{\varTheta_{\mathrm{ideal}}}\mathrm{d}\varTheta_{% \mathrm{ideal}}+\int\frac{nR}{C_{V}}\frac{1}{V}\mathrm{d}V$	$\displaystyle=0$
	$\displaystyle\int\frac{1}{\varTheta_{\mathrm{ideal}}}\mathrm{d}\varTheta_{% \mathrm{ideal}}+\frac{nR}{C_{V}}\int\frac{1}{V}\mathrm{d}V$	$\displaystyle=0$
	$\displaystyle\log_{e}\varTheta_{\mathrm{ideal}}+\frac{nR}{C_{V}}\log_{e}V+C_{1}$	$\displaystyle=0$
$C_{1}$ は定数
	$\displaystyle\log_{e}\varTheta_{\mathrm{ideal}}V^{\frac{nR}{C_{V}}}$	$\displaystyle=-C_{1}$
	$\displaystyle\varTheta_{\mathrm{ideal}}V^{\frac{nR}{C_{V}}}$	$\displaystyle=e^{-C_{1}}$
$e^{-C_{1}}=C_{2}$ と置き直す
	$\displaystyle\varTheta_{\mathrm{ideal}}V^{\frac{nR}{C_{V}}}$	$\displaystyle=C_{2}$

上式の右辺の $C_{2}$ は定数であるので、左辺の $\varTheta_{\mathrm{ideal}}V^{\frac{nR}{C_{V}}}$ は常に同じ値をとることが分かった。

常に同じ値をとることから、断熱過程の前後では等しくなると言える。この関係を断熱過程（2→3）で考えると次式を得る。

\displaystyle\varTheta_{\mathrm{ideal,12}}V_{2}^{\frac{nR}{C_{V}}}

\displaystyle=\varTheta_{\mathrm{ideal,34}}V_{3}^{\frac{nR}{C_{V}}}

(C.7)

同様に断熱過程（4→1）では次の関係が成り立つ。

\displaystyle\varTheta_{\mathrm{ideal,12}}V_{1}^{\frac{nR}{C_{V}}}

\displaystyle=\varTheta_{\mathrm{ideal,34}}V_{4}^{\frac{nR}{C_{V}}}

(C.8)

式(C.7)を式(C.8)で割り次の関係を得る。

	$\displaystyle\bigg{(}\frac{V_{2}}{V_{1}}\bigg{)}^{\frac{nR}{C_{V}}}$	$\displaystyle=\bigg{(}\frac{V_{3}}{V_{4}}\bigg{)}^{\frac{nR}{C_{V}}}$
	$\displaystyle\frac{V_{2}}{V_{1}}$	$\displaystyle=\frac{V_{3}}{V_{4}}$		(C.9)

C.2.3 熱の比

熱の比をこれまで求めた関係から導く。理想気体で構成されたカルノーサイクルの熱源と交換する熱の比を求めるため、式(C.4)を式(C.5)で割る。

	$\displaystyle\frac{Q_{34}}{Q_{12}}$	$\displaystyle=\frac{-nR\varTheta_{\mathrm{ideal,34}}\log_{e}\dfrac{V_{4}}{V_{3% }}}{-nR\varTheta_{\mathrm{ideal,12}}\log_{e}\dfrac{V_{2}}{V_{1}}}$
式(C.9)より分子分母の体積の比は同じである
	$\displaystyle\frac{Q_{34}}{Q_{12}}$	$\displaystyle=\frac{\varTheta_{\mathrm{ideal,34}}}{\varTheta_{\mathrm{ideal,12% }}}$	(C.10)

上式のように理想気体温度の比は可逆サイクルであるカルノーサイクルの熱源とやりとりする熱の比と等しいことが示せた。この関係は熱力学的絶対温度と同じ関係であるので、基準となる温度を等しくとれば（国際単位系（SI）第9版ではボルツマン定数[22]）同じ温度目盛りとなる。

C.1 温度の測定 References D 閉じた系のサイクルの付録

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。