1 熱力学第一法則とエネルギー 1.2 力学的エネルギー 1.4 熱力学第一法則

1.3 内部エネルギーと発熱、伝熱

内部エネルギーと発熱、伝熱は力学的エネルギーとは違うエネルギー形態である。どのようなエネルギーであるか見ていこう。

1.3.1 内部エネルギーと発熱

内部エネルギーと発熱は、昔から知られている仕事をした際にものが動く（運動エネルギーや位置エネルギーに変換される力学的エネルギーの保存）だけではなく、仕事をされたものが動きながら温度が上がる現象と関係している。例えば指で机をこする（指で机に仕事をする）と指と机が熱くなる現象がそうである。これは仕事が運動エネルギーや位置エネルギーとは異なる内部エネルギーへと変換されている。このとき仕事が内部エネルギーに不可逆に変換されるのを発熱と呼ぶ。発熱がおこり、内部エネルギーの上昇は温度上昇として現れる。内部エネルギーは系内の分子の運動エネルギーと分子同士の相互作用による位置エネルギーの総和であり、系の状態がわかれば決まる値である。エネルギーの保存式は内部エネルギー $U$ [J] の変化量 $\Delta U$ [J] を含め次のようになる。

\displaystyle W

\displaystyle=\Delta E_{\mathrm{運}}+\Delta E_{\mathrm{位}}+\Delta U

(1.7)

仕事から内部エネルギーへと変換される過程は、先ほど示した不可逆的な発熱と可逆的な変化の二種類に分けることが出来る。可逆的な変化は、元の状態に戻ることの出来る可逆的な系への仕事の作用によって系の内部エネルギーが上昇する過程である。例えば、摩擦や空気抵抗のない理想的なピストンの内部を系として考え、ピストンを押して系に仕事をする（図1.11）。すると、ピストン内部の系の温度と圧力が上昇し、内部エネルギーが仕事をされた分だけ上昇する。次にピストンを逆方向へ元の位置まで動かせば系は周囲に同じだけの仕事をして、内部エネルギーが低下し元の値まで温度も下がる。これが可逆的な系への仕事の作用の例である。

Figure 1.11: 可逆的な変化

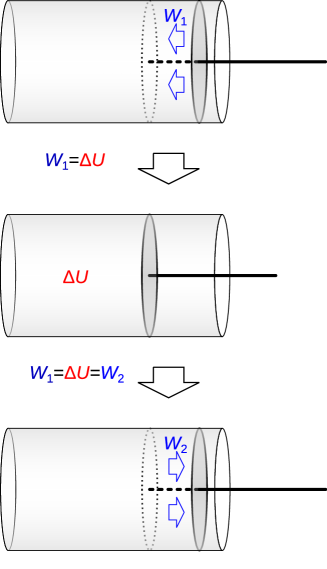
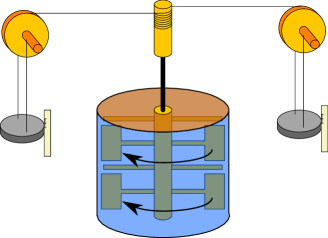
もう一つの過程では、仕事は不可逆的に系に作用する。この仕事から内部エネルギーへの不可逆的な作用を発熱と呼ぶ。よく熱力学で挙げられる例として、1850年にジュールにより報告された水槽の中に羽根車を入れて、羽根車を回転させ水に仕事をする実験[8]（図1.12）がある（水槽が系）⁴⁴4ジュールはこの実験でおもりの位置の変化から作用した仕事を計測し、温度上昇時の内部エネルギーの上昇量を明らかにした。。このとき、羽根車によって仕事をされた水槽の水は動き出すが、羽根車を止めた後に十分に長い時間待てば水は粘性により静止し温度は上昇する。静止した水は羽根車が回る前の水と運動エネルギー、位置エネルギー共に変化していない。羽根車から水に作用した仕事により水の内部エネルギーが変化している。この過程では逆の現象、水が動き出して板を押すということが起こることはないので、不可逆な現象である。この不可逆という考え方は熱力学で非常に重要な意味を持ち、時間の向きを決めるエントロピーへとつながる（詳細は後ろの熱力学第二法則の2章 ${}^{\text{p.\ref{sec-2ndLaw}}}$ で述べる）。発熱の他の例として、摩擦では異なる速度で運動している物体が接触した際に、互いに仕事が作用し速度が変わる。その仕事の一部が熱となり、物体の内部エネルギーが高くなり温度が上昇する現象が摩擦である。電気が流れる際にも電気抵抗のため電気エネルギーが熱に変換され、電気を流れている伝導体の内部エネルギーが高くなり温度が上昇する。この際の系に入ってきた電気エネルギーも仕事として捉えることが出来る。

Figure 1.12: ジュールの実験（文献[8]より）

現実の系への仕事の作用では可逆だけの作用はありえず、可逆の作用に摩擦などが混ざった不可逆の作用となる。可逆過程では逆の作用で元の状態（圧縮前）に戻るが、不可逆な作用が加わった場合には不可逆分だけ元の状態に戻すことができなくなる ⁵⁵5可逆と不可逆の仕事の作用は同じ仕事をして、同じだけ内部エネルギーが上昇しても、過程終了後の圧力や温度が異なる。仕事が完全に不可逆な変化で全て発熱した場合は、系は高温の物体から同量の熱が伝わった後と同じ状態となる。。

1.3.2 発熱がある場合の力学的エネルギーの変化

発熱がある場合の力学的エネルギーの変化はどのようになるだろうか。 1.2.4節 ${}^{\text{p.\ref{sec-MechanicalEnergy}}}$ で示した力学的エネルギーは保存され、可逆的に互いに変換される。しかし摩擦など発熱で内部エネルギーに変換された場合は簡単に元の力学的エネルギーに戻ることはできず不可逆な現象となる。熱を考えず力学的エネルギーの保存のみを考え可逆であった1.2.4節 ${}^{\text{p.\ref{sec-MechanicalEnergy}}}$ の図1.10 ${}^{\text{p.\ref{sec-MechanicalEnergy}}}$ と同じボールとバネで、熱への変換がある場合を考える（図1.13）。

Figure 1.13: 熱に変換されると不可逆となる

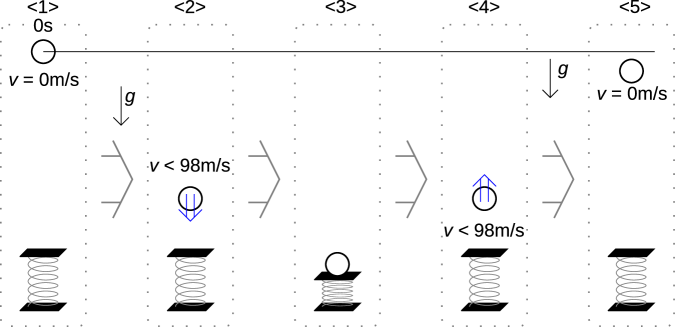
図1.13<1>ではボールは動いていないので位置エネルギーだけである。エネルギーの合計 $E_{合計}$ は次式で表される。

\displaystyle E_{合計}=E_{位1}

(1.8)

図1.13<2>では<1>に比べて位置エネルギーが減少し、減少分だけ運動エネルギーが増えている。ボールが空気中を落下する際には空気との摩擦や発生した空気の渦により、運動エネルギーの一部は熱となり、空気やボールの温度を上げ内部エネルギーの上昇 $\Delta U$ に使われる。エネルギーの合計 $E_{合計}$ は次のようになる。

\displaystyle E_{合計}=E_{位2}+E_{運2,熱}+\Delta U_{2}

(1.9)

力学的エネルギーのみの場合の式(1.3)と比べて、同じ位置（同じ位置エネルギー $E_{位2}$ ）では内部エネルギーが上昇した分（ $\Delta U_{2}$ ）だけ運動エネルギーが小さく（ $E_{運2,熱}<E_{運2}$ ）、速度が遅くなることがわかる。

図1.13<3>では速度は0で位置エネルギーの基準をこの位置ととれば、エネルギーの合計 $E_{合計}$ はバネのエネルギーと温度上昇分の内部エネルギーの変化分であり、次のように表される。この時のバネのエネルギーは力学的エネルギーのみの場合の式(1.4)のバネのエネルギーよりも内部エネルギーの変化分（ $\Delta U_{3}$ ）だけ小さくなる（ $E_{バネ3,熱}<E_{バネ3}$ ）。

\displaystyle E_{合計}=E_{バネ3,熱}+\Delta U_{3}

(1.10)

図1.13<4>では位置が<2>と同じとする（ $E_{位4}=E_{位2}$ ）と、さらに空気の摩擦などにより内部エネルギーの変化量が増えており（ $\Delta U_{4}>\Delta U_{2}$ ）、運動エネルギーはさらに小さく（ $E_{運4,熱}<E_{運2,熱}<E_{運2}$ ）、速度もさらに遅い。

\displaystyle E_{合計}=E_{位4}+E_{運4,熱}+\Delta U_{4}

(1.11)

図1.10<5>では内部エネルギーに変化した分（ $\Delta U_{5}$ ）だけ位置エネルギーは小さく、<1>よりも低い位置で速度がゼロとなる。

\displaystyle E_{合計}=E_{位5}+\Delta U_{5}

(1.12)

現実におこっているように力学的エネルギーが熱から内部エネルギーへ変換される場合には、現象は不可逆となる。時間を逆に<5>→<4>→<3>→<2>→<1>と動かした場合、初めの位置よりも高くボールが持ち上がることはありえず、不可逆な現象であり、時間の進む向きは明らかである。ボールが跳ね続ければ、ボールの力学的エネルギーは全て空気抵抗などで熱に変換され、ボールや周囲の温度が高くなり、ボールの運動は止まる。

1.3.3 伝熱

伝熱、すなわち熱が伝わることでもエネルギーが受け渡される。仕事の作用がなくても系の周囲の温度が系と異なれば、系の温度と周囲の温度が変化し近づいていくことを我々は経験的に知っている。このとき、系の温度が変わり系の内部エネルギーも変化している。この温度差により伝わるエネルギーを熱と呼ぶ。熱は温度差のある物体間で伝わるエネルギー伝達の形態の一つである。伝わった熱は内部エネルギーに変換され仕事や位置エネルギー、運動エネルギーになることはない。熱が伝わる際には温度差があり、熱は温度の高いところから低いところへ伝わる。この熱の伝わりも、時間を逆に進めた現象（低温から高温に熱が伝わる）はありえないので、不可逆な現象である。

仕事が作用しない系で、位置エネルギーと運動エネルギーが変化しない条件下での、内部エネルギーの変化が熱の作用である。その際の伝わった熱 $Q$ [J] と内部エネルギーの変化量 $\Delta U$ [J] の関係は次式で表される（熱が系に入ってくる際の符号が正となるよう定義する）。

\displaystyle Q=\Delta U

(1.13)

図1.14「状態１」のように温度 $T_{\mathrm{H1}}$ [℃またはK]の高温の物体と温度 $T_{\mathrm{L1}}$ [℃またはK]の低温の物体を接触させ（ $T_{\mathrm{H1}}>T_{\mathrm{L1}}$ ）、図1.14「状態２」の温度 $T_{\mathrm{H2}}$ [℃またはK]と温度 $T_{\mathrm{L2}}$ [℃またはK]まで変化した際に、高温の物体から低温の物体に伝わった熱 $Q_{12}$ [J]と高温の物体の内部エネルギー $U_{\mathrm{H1}}$ 、 $U_{\mathrm{H2}}$ 、低温の物体の内部エネルギー $U_{\mathrm{L1}}$ 、 $U_{\mathrm{L2}}$ は次の関係となる（高温物体は熱が出ていく方向のため負号がつく ⁶⁶6熱の符号は系に対しての向きで決まるため、高温物体を系とした場合と低温物体を系とした場合で別々に $Q$ を表し符号を逆としなくてはならないが、煩雑になるため絶対値でまとめて表した。）。

\displaystyle-(U_{\mathrm{H2}}-U_{\mathrm{H1}})=|Q_{12}|=U_{\mathrm{L2}}-U_{% \mathrm{L1}}

(1.14)

高温の物体は「状態１」から「状態２」への変化で内部エネルギーは減少し温度も低下する（図1.14では $T_{\mathrm{H1}}$ [℃またはK]から $T_{\mathrm{H2}}$ [℃またはK]、 $T_{\mathrm{H1}}>T_{\mathrm{H2}}$ ）。低温の物体では内部エネルギーが上昇し温度も上昇する（図1.14では $T_{\mathrm{L1}}$ [℃またはK]から $T_{\mathrm{L2}}$ [℃またはK]、 $T_{\mathrm{L1}}<T_{\mathrm{L2}}$ ）。温度の異なる物体を十分に長い時間接触させると、二つの物体の温度は等しくなる（ $T_{\mathrm{H3}}=T_{\mathrm{L3}}$ ）。この図1.14「状態３」を熱平衡状態と呼ぶ。

Figure 1.14: 内部エネルギー・熱平衡

1.3.4 熱容量と比熱

熱容量と比熱で内部エネルギーと温度の関係を表すことができる。仕事による発熱や熱を受け取り内部エネルギーが増えると温度が上昇する⁷⁷7蒸発や融解などの相変化のない単相から成り立つ系において。。熱 $Q$ [J] のみを受け取り仕事の作用がない系の体積が一定である条件での、内部エネルギーの変化量 $\Delta U$ [J] と温度の変化量 $\Delta T$ [K] の関係を等積熱容量 $C_{V}$ [J/K] で次のように表される。

	$\displaystyle\Delta U$	$\displaystyle=C_{V}\Delta T$
	$\displaystyle C_{V}$	$\displaystyle=\frac{\Delta U}{\Delta T}$

通常、この等積熱容量 $C_{V}$ [J/K] は温度によって変化するので、 $\Delta T$ の温度変化でも値が変わる。ある温度での値を求めるために、 $\Delta T$ のゼロの極限を取り偏微分の形で次のように表す。

\displaystyle C_{V}=\dfrac{\partial U}{\partial T}

(1.15)

また、系の質量を $m$ [kg] とし上式(1.15)の両辺を質量 $m$ [kg] で割ることで、質量あたりの内部エネルギーの変化を表す等積比熱 $c_{V}$ [J/(kg K)] を次式のように表すことが出来る ⁸⁸8等積比熱とは体積の変化しない状態で単位質量（1 kg）の物体を単位温度（1 ℃）上昇させるのに必要なエネルギー量である。。熱力学では質量あたりを表す際に「比」をつける。熱容量に「比」をつけて比熱容量、これを短くして比熱と呼ばれる。

\displaystyle c_{V}=\frac{1}{m}\dfrac{\partial U}{\partial T}

等積比熱 $c_{V}$ [J/(kg K)] は物質の状態 ⁹⁹9温度、圧力などで表される。が決まれば値が決まる物性値である。温度の変化に対する変化が十分に小さく一定とみなすことが出来れば ¹⁰¹⁰10等積比熱などの物性値は温度と圧力で値が変化するが、ここではその変化量が小さいために一定とみなせるとする。、温度変化 $\Delta T$ [℃またはK] による内部エネルギーの変化量 $\Delta U$ [J] は次式で表される。

\displaystyle\Delta U=c_{V}m\Delta T

(1.16)

比熱を使って図1.14の温度変化から内部エネルギーの変化を計算できる。図1.14のように2つの物体を接触させると、伝わった熱 $Q$ [J]の分だけ、質量 $m_{\mathrm{H}}$ [kg]で等積比熱 $c_{V\mathrm{,H}}$ [J/(kg $\cdot$ K)]の高温の物体の内部エネルギーは $U_{\mathrm{H1}}$ [J]から $U_{\mathrm{H2}}$ [J]に減少し( $U_{\mathrm{H1}}>U_{\mathrm{H2}}$ )、質量 $m_{\mathrm{L}}$ [kg]で等積比熱 $c_{V\mathrm{,L}}$ [J/(kg $\cdot$ K)]の低温の物体の内部エネルギーは $U_{\mathrm{L1}}$ [J]から $U_{\mathrm{L2}}$ [J]に増加する( $U_{\mathrm{L1}}<U_{\mathrm{L2}}$ )。この内部エネルギーの変化量に応じて、物体の温度が変化する。高温物体の内部エネルギーの変化（減少） $\Delta U_{\mathrm{H}}$ [J]は次式より求まる ¹¹¹¹11 $\Delta$ で表される変化量は変化後から変化前を引くことで求められる。前後の順番が分からなくなった時は、量が増加した場合は正の値となり、減少した場合は負の値となる順番にすると正しい式となる。。

\displaystyle\Delta U_{\mathrm{H}}=U_{\mathrm{H2}}-U_{\mathrm{H1}}=\int^{T_{% \mathrm{H2}}}_{T_{\mathrm{H1}}}c_{V\mathrm{,H}}m_{\mathrm{H}}\mathrm{d}T=m_{% \mathrm{H}}\int^{T_{\mathrm{H2}}}_{T_{\mathrm{H1}}}c_{V\mathrm{,H}}\mathrm{d}T<0

温度の変化に対して等積比熱 $c_{V}$ [J/(kg K)] を一定とみなすことが出来れば、次式より求まる。

\displaystyle\Delta U_{\mathrm{H}}=U_{\mathrm{H2}}-U_{\mathrm{H1}}=c_{V\mathrm% {,H}}m_{\mathrm{H}}(T_{\mathrm{H2}}-T_{\mathrm{H1}})<0

(1.17)

低温物体の内部エネルギーの変化（増加） $\Delta U_{\mathrm{L}}$ [J] も同様に次式より求まる。

\displaystyle\Delta U_{\mathrm{L}}=U_{\mathrm{L2}}-U_{\mathrm{L1}}=\int^{T_{% \mathrm{L2}}}_{T_{\mathrm{L1}}}c_{V\mathrm{,L}}m_{\mathrm{L}}\mathrm{d}T=m_{% \mathrm{L}}\int^{T_{\mathrm{L2}}}_{T_{\mathrm{L1}}}c_{V\mathrm{,L}}\mathrm{d}T>0

温度の変化に対して等積比熱 $c_{V}$ [J/(kg K)] を一定とみなすことが出来れば、次式より求まる。

\displaystyle\Delta U_{\mathrm{L}}=U_{\mathrm{L2}}-U_{\mathrm{L1}}=c_{V\mathrm% {,L}}m_{\mathrm{L}}(T_{\mathrm{L2}}-T_{\mathrm{L1}})>0

(1.18)

1.3.5 まとめ

まとめとして、内部エネルギーは系の持っているエネルギーであり、発熱は仕事から内部エネルギーへの不可逆的なエネルギーの変化、伝熱は物体間に温度差がある場合ある物体から別の物体へと伝わるエネルギーである。熱の移動は温度の差がある場合だけに起こり、物質や大きさが違えば温度が同じでも内部エネルギーが違うこともありえるが、内部エネルギーの差では熱の移動は起こらない。また温度の低い物体から温度の高い物体へ熱は伝わらないため、熱が伝わる現象は不可逆である。

これまでに示した温度の変化の際の内部エネルギーの変化を、温度変化として顕（あらわ）れているので顕熱と言う。内部エネルギーには温度変化による顕熱の他に、固相から液相、液相から気相のように相変化をした際の内部エネルギーの変化である潜熱も含まれる。固相から液相、液相から気相への相変化では潜熱により内部エネルギーが増加し、気相から液相、液相から固相への変化では内部エネルギーは減少する。水の加熱を例に挙げると、鍋で水を沸かす場合、常温から水に熱を加えると大気圧下での水の沸点温度100 ℃まで加えられた熱は顕熱として内部エネルギーが変化し温度が上昇する。温度が100 ℃に到達すると熱を加えても温度は変化せず、加えられた熱により潜熱として内部エネルギーが変化し液相の水が気相の蒸気へと相変化する。水が全て蒸気へと変化すると、鍋の場合には拡散して空気と混ざってしまうが、密閉した容器であれば再度加えられた熱は顕熱として内部エネルギーが変化し温度が上昇する。水を液相から気相へ相変化させるのに必要な潜熱は大気圧下で単位質量あたりで2257 kJ/kg [18]である。等積比熱が4.130 kJ/(kg K) [18]であるので、1 kgの水を沸騰させるのに必要なエネルギーで約546 kgの水の温度を1 ℃上げることができる。水1 kgの潜熱に相当する力学的エネルギーは、約2000 kgの物体を重力下で約115 m持ち上げる位置エネルギーと同程度である。

1.2 力学的エネルギー References 1.4 熱力学第一法則

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。