1 熱力学第一法則とエネルギー 1.1 系と境界 1.3 内部エネルギーと発熱、伝熱

1.2 力学的エネルギー

力学的エネルギーが色々なエネルギーの中でも一番想像がしやすいだろう。エネルギーの中でも、仕事や運動エネルギー、位置エネルギーといった運動に関係する力学的エネルギーを定義するところからはじめよう。

1.2.1 仕事

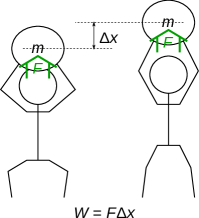
「仕事＝力×距離」の関係（図1.3）から、エネルギーの単位J（ジュール）が力の単位N（ニュートン）かける距離の単位m（メートル）でSI（国際単位系）において組み立てられている[22]ように、仕事からエネルギーを定義しよう。例えばものを持ち上げれる時には、下に向かう重力に逆らって上向きに力を加え、ものに仕事が作用する（図1.3）。床に置いてある荷物を動かすときには、床との摩擦力に対抗する力で荷物を押す必要があり、ここでも仕事が荷物に作用する。このように仕事は力を加えてものを動かした際に作用する。仕事 $W$ [J]は、力 $F$ [N]を加えながら移動した距離 $\Delta x$ [m]により、次式の様に計算される。

W=F\Delta x

加わっている力が移動する間一定の大きさであれば上式で良いが、力の大きさが変化することもあるだろう。その際には次のように微小な移動距離 $\mathrm{d}x$ [m]での微小仕事 $\delta W$ [J]として次のように計算する ¹¹1力 $F$ は $x$ の関数とは限らないため微小な仕事は連続関数の微小な変化ではない。不完全微分方程式であるので、”d”ではなく” $\delta$ ”で微小量を表す。A.1節 ${}^{\text{p.\ref{sec-WorkInexact}}}$ に詳細を示す。。

\displaystyle\delta W=F\mathrm{d}x

(1.1)

上式を移動した区間（ここでは位置１から位置２）で積分すると、その間に作用した仕事の大きさが計算できる。

\displaystyle W=\int^{2}_{1}F\mathrm{d}x

Figure 1.2: 仕事の定義

Figure 1.3: 重力に対する仕事

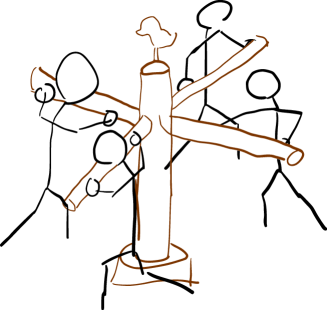
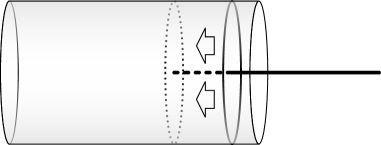
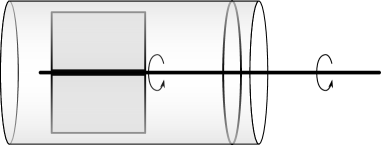
仕事が作用する際の移動は直線だけでなく、回転による移動でもよい（図1.4）。回転では場所を移動しないため、扇風機やタービンのように同じ場所で仕事の作用を続ける場合に都合が良い。扇風機は空気に対して回転しながら力を加えつづけることで仕事をし、連続的に空気の流れを作っている。系に作用する仕事も、式(1.1)での $\mathrm{d}x$ の移動の仕方により二通りに分けることができる。一つは系の境界に力が加わり系の形（体積）が変わったことにより直線的に $\mathrm{d}x$ 移動する仕事であり、ピストン形状の系での体積変化が典型例である（図1.6）。もう一つは系の内部で系の一部に力が加わり回転しながら $\mathrm{d}x$ 動くことによる仕事であり、例として系の内部にプロペラがあり系の外からプロペラの軸の回転で力を伝え仕事が作用するような系が挙げられる（図1.6）。

Figure 1.4: 回転による仕事

Figure 1.5: 並進運動による仕事

Figure 1.6: 回転運動による仕事

仕事は、ある物体から別の物体へ力が作用した際に伝わるエネルギーの形態であり、作用した後は力を加えられた物体の保有する運動エネルギーや位置エネルギーとなる。

1.2.2 運動エネルギー

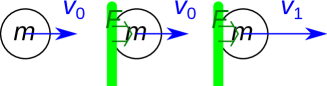
運動エネルギーは動いている物体が持っているエネルギーである。床の上の荷物に力を加え仕事を作用させると動き出す。このとき熱力学第一法則からエネルギーが保存され、仕事は運動エネルギーへと変わることから運動エネルギーの大きさを求めていく。図1.7のように、速度 $v_{0}$ [m/s]で運動している（状態0）質量 $m$ [kg]の物体に力 $F$ [N]で仕事 $W_{01}$ [J]をして速度が $v_{1}$ [m/s]に変化した際（状態1）のエネルギーの変化を示す。状態0での運動エネルギー $E_{運,0}$ [J]からされた仕事分 $W_{01}$ [J]だけ運動エネルギーが増加し、状態1での運動エネルギー $E_{運,1}$ [J]となる。

	$\displaystyle E_{運,1}-E_{運,0}$	$\displaystyle=W_{01}\hskip 60.0pt状態0から状態1までの区間で積分$
		$\displaystyle=\int_{0}^{1}\delta W\hskip 40.0ptここで式\eqref{eq-Work}で変形$
		$\displaystyle=\int_{0}^{1}F\mathrm{d}x\hskip 35.0ptここで力の定義であるF=m\frac{\mathrm{% d}v}{\mathrm{d}t}を代入$
		$\displaystyle=\int_{0}^{1}m\frac{\mathrm{d}v\mathrm{d}x}{\mathrm{d}t}\hskip 20% .0ptここで\dfrac{\mathrm{d}x}{\mathrm{d}t}=vで変形$
		$\displaystyle=\int_{0}^{1}mv\mathrm{d}v$
		$\displaystyle=m\int_{0}^{1}v\mathrm{d}v$
		$\displaystyle=m\biggl{[}\frac{1}{2}v^{2}\biggr{]}_{0}^{1}$
		$\displaystyle=\frac{1}{2}mv_{1}^{2}-\frac{1}{2}mv_{0}^{2}$

この $\dfrac{1}{2}mv^{2}$ [J]が運動エネルギーである。仕事をされることにより物体の運動エネルギーは増加する。

Figure 1.7: 運動エネルギー

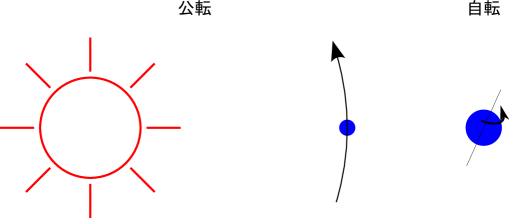
運動エネルギーは直線的な運動（並進運動）だけではなく、太陽の周りを回る地球のように円運動（公転）をしている物体や、地球の自転のように回転している物体も保有している（図1.8） ²²2 角速度 $\omega$ により回転している物体の回転による運動エネルギーを次式のように表すことができる。 $\displaystyle E_{運,回}=\int\frac{1}{2}r^{2}\omega^{2}\mathrm{d}m$ 回転は重心を通る軸を中心とする。物体形状と軸の向きで、同じ回転速度でもエネルギーが異なる。。

Figure 1.8: 回転による運動エネルギー

1.2.3 位置エネルギー

位置エネルギーは重力や電磁気力によるエネルギーである。身の回りで多く扱われるのは重力による位置エネルギーである。ここでも位置エネルギーとだけ書いた場合は重力による位置エネルギーとする。

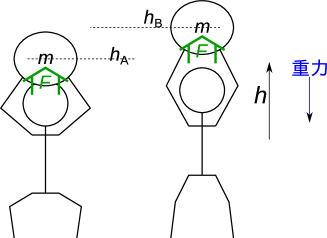
重力による位置エネルギーの変化を作用する仕事から求める。質量 $m$ の物体は重力下では常に $m g$ の力を受ける（ $g$ [m/s²]は重力加速度9.81 m/s²）。力の向きとは逆方向に座標 $h$ をとり、ある位置A（ $h_{\mathrm{A}}$ ）からある位置B（ $h_{\mathrm{B}}$ ）まで質量 $m$ の物体を移動させると、位置Bでの位置エネルギー $E_{\mathrm{位,B}}$ は移動の際にされた仕事の分だけ位置Aでの位置エネルギー $E_{\mathrm{位,A}}$ よりも大きくなる（図1.9）。

	$\displaystyle E_{\mathrm{位,B}}-E_{\mathrm{位,A}}$	$\displaystyle=mg(h_{\mathrm{B}}-h_{\mathrm{A}})$
		$\displaystyle=mgh_{\mathrm{B}}-mgh_{\mathrm{A}}$

上式の $m g h$ が重力による位置エネルギーである。詳細な説明は付録A.2節 ${}^{\text{p.\ref{sec-PotentialEnergy}}}$ でしている。

Figure 1.9: 位置エネルギー

1.2.4 力学的エネルギーの保存

力学的エネルギーの保存についてまず例を見てみよう。実際の運動には必ず熱がともなうため、実際にはありえない理想的な条件である。

バネの上でボールが跳ねる、力学的エネルギーが保存される理想的な場合の例を図1.10に示す。ここでは理想的なバネを考え、 $l$ [m]押された場合に $F=kl$ の力がかかるとする（ $k$ [N/m]はばね定数で一定とする）。³³3この時、バネに蓄えられるエネルギーは次式で表される。 $\displaystyle E_{バネ}$ $\displaystyle=\int^{l}_{0}Fdl$ $\displaystyle=\int^{l}_{0}kldl$ $\displaystyle=\frac{1}{2}kl^{2}$

Figure 1.10: 力学的エネルギーの保存

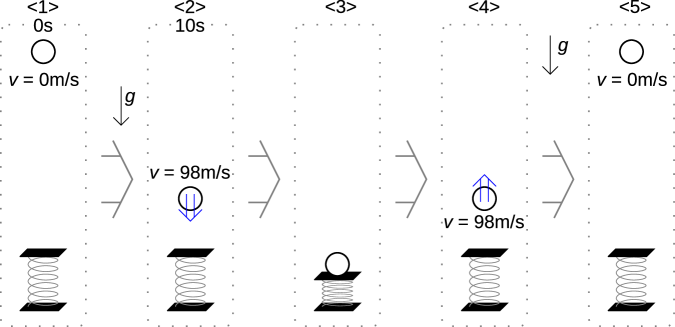
図1.10<1>ではボールは動いていないので位置エネルギーだけである。力学的エネルギーの合計 $E_{合計}$ は次式で表される。

\displaystyle E_{合計}=E_{位1}

(1.2)

図1.10<2>では<1>に比べて位置エネルギーが減少し、減少分だけ運動エネルギーが増えている。力学的エネルギーの合計 $E_{合計}$ は次のようになる。

\displaystyle E_{合計}=E_{位2}+E_{運2}

(1.3)

図1.10<3>では速度は0で位置エネルギーの基準をこの位置ととれば、力学的エネルギーの合計 $E_{合計}$ はバネのエネルギーのみであり、次のように表される。

\displaystyle E_{合計}=E_{バネ3}

(1.4)

図1.10<4>は<2>と同じ位置で、速度は<2>の逆向きで同じ大きさとなった時であり、位置エネルギーと運動エネルギーは等しい。

\displaystyle E_{合計}=E_{位4}+E_{運4}=E_{位2}+E_{運2}

(1.5)

図1.10<5>では<1>とぴったり同じ位置で速度0となる。

\displaystyle E_{合計}=E_{位5}=E_{位1}

(1.6)

力学的エネルギーが保存される理想的な条件では、この<1>から<5>の運動が繰り返される。また、この例では現象は可逆であり、時間を逆に<5>→<4>→<3>→<2>→<1>と動かしたとしても正しい時間の方向<1>→<2>→<3>→<4>→<5>との区別はできない。力学的エネルギーだけの理想的な状況を考える場合には熱が関わらないため、時間の方向が定まらない。

1.1 系と境界 References 1.3 内部エネルギーと発熱、伝熱

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。