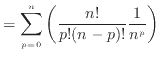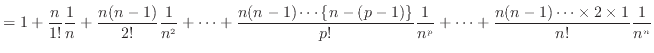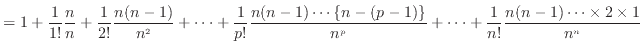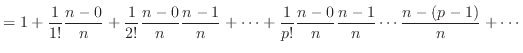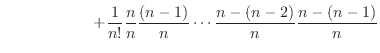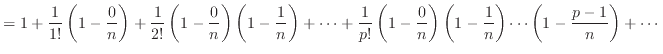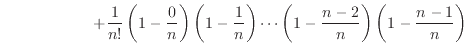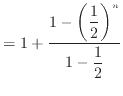

Next: A..4 指数関数の例
Up: A. おまけ
Previous: A..2.3 底の変換
自然対数の底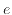 の定義を確認する。自然対数の底である
の定義を確認する。自然対数の底である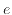 は、微分しても元の関数と同じ形になる次式が成り立つ定数
は、微分しても元の関数と同じ形になる次式が成り立つ定数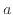 を
を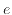 としている。
としている。
式(15)の左辺を微分の定義に沿って計算する。
定式から式(15)が成り立つには次式(16)の関係が成り立てば良い。この次式(16)を変形し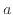 の値を求める。
の値を求める。
上式(17)の条件を満たす定数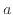 が
が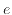 である。
である。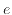 の式として再度示す。
の式として再度示す。
上式で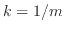 (
(
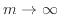 )とすれば次のようにも表される。
)とすれば次のようにも表される。
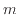 に対する
に対する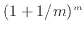 のグラフを図13に示す。グラフの範囲では
のグラフを図13に示す。グラフの範囲では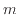 が大きくなると2.7より少し上に収束するように見える。
が大きくなると2.7より少し上に収束するように見える。
図 13:
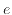 の収束
の収束
|
|
式(18)が収束するか確認する。そのために数列
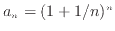 の極限を求める。この極限が収束すれば式(18)も収束する。
の極限を求める。この極限が収束すれば式(18)も収束する。
上式(19)より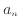 の各項は
の各項は と共に単調に増加し、全ての項が正であるので、
と共に単調に増加し、全ての項が正であるので、 は単調に増加する。次に
は単調に増加する。次に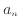 が上に有界であることを示す。
式(19)で
が上に有界であることを示す。
式(19)で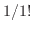 、
、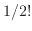 、・・・、
、・・・、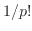 、・・・、
、・・・、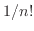 と掛けあわせている
と掛けあわせている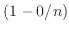 、
、
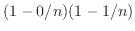 、・・・、
、・・・、
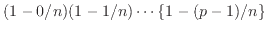 、・・・、
、・・・、
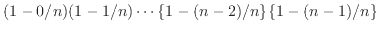 の
の
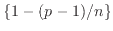 のような各括弧内は1から1よりも小さい正数を引いているので1以下の値となる。この1以下の値を掛けているのでため、各項の値はそれぞれ
のような各括弧内は1から1よりも小さい正数を引いているので1以下の値となる。この1以下の値を掛けているのでため、各項の値はそれぞれ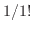 、
、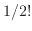 、・・・、
、・・・、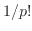 、・・・、
、・・・、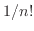 よりも小さい。各項の和である
よりも小さい。各項の和である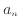 も
も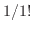 、
、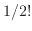 、・・・、
、・・・、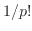 、・・・、
、・・・、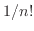 の和よりも小さくなるため次のように書ける。
の和よりも小さくなるため次のように書ける。
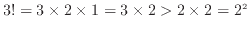 、
、
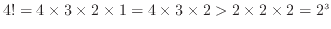 、
、
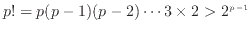 であるので、その逆数の関係と式(20)より次式が成り立つ。
であるので、その逆数の関係と式(20)より次式が成り立つ。
以上より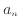 が上に有界であると示すことが出来た。
が上に有界であると示すことが出来た。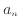 は単調に増加し上に有界であるので、極限はある値に収束する。よって式(18)で表される
は単調に増加し上に有界であるので、極限はある値に収束する。よって式(18)で表される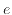 も収束する。
も収束する。


Next: A..4 指数関数の例
Up: A. おまけ
Previous: A..2.3 底の変換
関連する記事
・この記事の新しい版
対数グラフ 2020.03.25版
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。
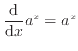
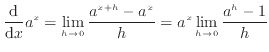
![]() に対する
に対する![]() のグラフを図13に示す。グラフの範囲では
のグラフを図13に示す。グラフの範囲では![]() が大きくなると2.7より少し上に収束するように見える。
が大きくなると2.7より少し上に収束するように見える。
![]() の極限を求める。この極限が収束すれば式(18)も収束する。
の極限を求める。この極限が収束すれば式(18)も収束する。
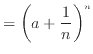 二項定理より
二項定理より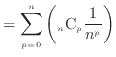 Cの定義より
Cの定義より