

Next: 参考文献
Up: A. おまけ
Previous: A..3 自然対数の底
対数は一定数増えていく"+"の現象ではなく、ある倍数で増えていく"×"の現象を考える際に便利である。例えば池の中のプランクトンが一日で二倍に増える時の数は指数関数で次のような式で表される。
プランクトンの一日経過後の関係は次式となる。
| |
(プランクトンの数2日目)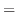 (プランクトンの数1日目) (プランクトンの数1日目)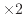 |
|
定式から経過日数とプランクトンの関係は次のように指数関数となる。
| |
(プランクトンの数)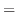 (プランクトンの数1日目) (プランクトンの数1日目)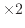 日数 日数 |
|
銀行のお金がある金利で増える時の額の一年経過後の関係は以下のとおりである。
| |
(次年の額)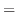 (今年の額) (今年の額)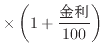 |
|
現在の額と年数の関係は次のような指数関数となる。
| |
(現在の額)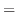 (元金) (元金)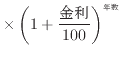 |
|
自分の祖先の数は同様に次の関係となる。
| |
(おじいちゃん・おばあちゃんの人数)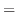 (お父さん・お母さんの人数) (お父さん・お母さんの人数)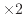 |
|
| |
(祖先の人数)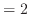 代 代 |
|
ここでは祖先の数と代の関係が指数関数となっている。
元金10 000円で年利1%で貯金したとき20 000円になるには何年かかるかを対数で計算できる。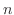 年かかるとすると次式で表される。
年かかるとすると次式で表される。
両辺を1.01が底の対数をとる。
計算機で
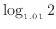 の計算をすれば、約70年で二倍となることがわかる。また、2.1.2節で述べたように片対数グラフ上では直線として描かれる。
の計算をすれば、約70年で二倍となることがわかる。また、2.1.2節で述べたように片対数グラフ上では直線として描かれる。
対数については「指数・対数のはなし?異世界数学への旅案内」[1]を読むことをお勧めする。対数のおもしろさを知ることができる。


Next: 参考文献
Up: A. おまけ
Previous: A..3 自然対数の底
関連する記事
・この記事の新しい版
対数グラフ 2020.03.25版
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。
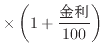
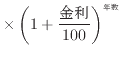
![]() 年かかるとすると次式で表される。
年かかるとすると次式で表される。