＜戻る: 2.2 対数軸＞   ＜次へ: A. おまけ＞


3 対数グラフでの変化

3.1 対数グラフでの見え方の違い

それぞれの対数グラフで色々な関数がどのように描かれるかを示す。測定した実験データを処理することを想定し測定値が一定量ずれていた場合に、それがどのようにグラフに反映されるかも見てみる。

3.1.1 線形-対数 片対数グラフ

線形-対数グラフで直線で表された次の指数関数の式を基本とする。

$\displaystyle y$ $\displaystyle = 0.9 \times 1.1^x$ (2)

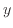$ x$ 方向に10ずらした式(6)、$ y$ 方向に1000ずらした式(7)、定数をそれぞれ変えた式(8)と式(9)でグラフが元の形からどう変わるか見ていく。

$\displaystyle y$ $\displaystyle = 0.9 \times 1.1^{(x - 10)}$ (6)
$\displaystyle y$ $\displaystyle = 0.9 \times 1.1^x + 1000$ (7)
$\displaystyle y$ $\displaystyle = 3 \times 1.1^x$ (8)
$\displaystyle y$ $\displaystyle = 10^{-6} \times 1.3^x$ (9)

図 10: 線形-対数グラフでの比較（線形）
\includegraphics[width=70mm]{figures/Graph_io-ii.eps}

図 11: 線形-対数グラフでの比較（片対数）
\includegraphics[width=70mm]{figures/Graph_io-io.eps}

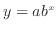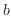表1に示すように、片対数グラフ（線形-対数）では指数関数$ y = a b^x$ に対して傾きが $ \log_{10} b$ 、切片が $ \log_{10} a$ として表される。図11でも$ b$ の値が異なる赤線（式(9)）のみ傾きが大きくなっている。また、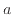$ a$ の値が異なる緑線（式(8)）では切片が違うことが見て取れる。グラフから傾きと切片を読み取ることでどのような関数か知ることができる。

3.1.2 対数-対数　両対数グラフ

対数-対数グラフで直線で表された次のべき関数の式を基本とする。

$\displaystyle y$ $\displaystyle = 0.8 x ^2$ (4)

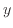$ x$ 方向に5ずらした式(10)、$ y$ 方向に1000ずらした式(11)、定数をそれぞれ変えた式(12)と式(13)がどう変わるか見ていく。

$\displaystyle y$ $\displaystyle = 0.8 (x - 5)^2$ (10)
$\displaystyle y$ $\displaystyle = 0.8 x^2 + 1000$ (11)
$\displaystyle y$ $\displaystyle = 1.3 x^2$ (12)
$\displaystyle y$ $\displaystyle = 0.01 x^3$ (13)

図 12: 対数-対数グラフでの比較（線形）
\includegraphics[width=70mm]{figures/Graph_oo-ii.eps}

図 13: 対数-対数グラフでの比較（両対数）
\includegraphics[width=70mm]{figures/Graph_oo-oo.eps}

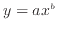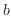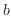表1に示すように、両対数グラフ（対数-対数）ではべき関数$ y = a x^b$ に対して傾きが$ b$ 、切片が $ \log_{10} a$ として表される。図13でも$ b$ の値が異なる赤線（式(13)）のみ傾きが大きくなっている。また、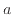$ a$ の値が異なる緑線（式(12)）では切片が違うことが見て取れる。両対数グラフではべき関数がどのような関数かグラフから傾きと切片を読み取ることで知ることができる。


＜戻る: 2.2 対数軸＞   ＜次へ: A. おまけ＞

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。