<戻る: 3.1 対数グラフでの見え方の違い>
<次へ: A..2 対数グラフでの変化の詳細計算>
A..1 詳細な計算
「1 対数グラフと線形グラフの性質」で示した以下のそれぞれの関数についての計算の詳細を示す。
線形関数 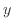 |
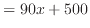 |
(1) |
指数関数 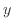 |
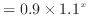 |
(2) |
対数関数 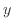 |
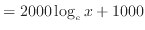 |
(3) |
べき関数 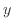 |
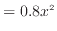 |
(4) |
対数軸では値の 、
、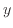 に対して10の対数を取った次式で表される
に対して10の対数を取った次式で表される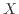 、
、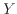 との関係が表される。
との関係が表される。
上式を変形する。
この関係を対数軸をとる変数へ代入し、対数軸では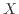 、
、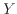 、通常の軸では
、通常の軸では 、
、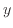 との関係を見ればどのような形のグラフとなるか分かる。
式(1)~式(4)の関数のそれぞれのグラフへの対応を見ていく。
との関係を見ればどのような形のグラフとなるか分かる。
式(1)~式(4)の関数のそれぞれのグラフへの対応を見ていく。
対数軸がない通常の線形グラフでは図14に示すように黒線の線形関数(式(1))は直線に、青線の指数関数(式(2))は下に凸の曲線に、緑線の対数関数(式(3))は上に凸の曲線に、赤線のべき関数(式(4))は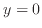 に対して対称な下に凸の曲線になる。対数
に対して対称な下に凸の曲線になる。対数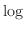 はゼロ以下の値には使えないため、対数関数は
はゼロ以下の値には使えないため、対数関数は が正の領域のみ曲線が描かれる。
が正の領域のみ曲線が描かれる。
A..1.2 線形-対数 片対数グラフ
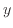 軸が対数の片対数グラフでは式(1)~式(4)の関数は図15のように描かれる。
軸が対数の片対数グラフでは式(1)~式(4)の関数は図15のように描かれる。
線形関数の式(1)を変形する。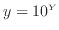 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
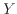 と
と は対数関数に近い形となり、図15の線形関数を表す黒線は線形-線形グラフ(図14)の対数関数(緑線)と近い上に凸の曲線になっている。
は対数関数に近い形となり、図15の線形関数を表す黒線は線形-線形グラフ(図14)の対数関数(緑線)と近い上に凸の曲線になっている。
指数関数の式(2)を変形する。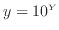 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
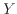 と
と が線形の式となっているので、図15の指数関数を表す青線は直線となっている。縦軸は対数であるので、10倍になると
が線形の式となっているので、図15の指数関数を表す青線は直線となっている。縦軸は対数であるので、10倍になると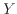 が1増加する。変換後の式から、
が1増加する。変換後の式から、 が100増加すると、
が100増加すると、
 は4.139増加することが分かり、グラフ(図15)でも、
は4.139増加することが分かり、グラフ(図15)でも、 が100増加すると、
が100増加すると、
 は4.139増加している。定数
は4.139増加している。定数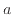 、
、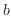 で表した指数関数の同様な変形は次式のようになる。
で表した指数関数の同様な変形は次式のようになる。
グラフから読みとれる傾きが
 、切片が
、切片が
 である(表1)。このことから読みとった傾きと切片から元の関数の
である(表1)。このことから読みとった傾きと切片から元の関数の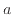 と
と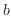 を求めることが出来る。
を求めることが出来る。
対数関数の式(3)を変形する。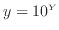 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
図15に示すように対数関数を表す緑線は上に凸の曲線となる。
べき関数の式(4)を変形する。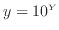 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
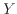 と
と は対数関数となり、図15のべき関数を表す赤線は線形-線形グラフ(図14)の対数関数(緑線)と近い上に凸の曲線になっている。
は対数関数となり、図15のべき関数を表す赤線は線形-線形グラフ(図14)の対数関数(緑線)と近い上に凸の曲線になっている。
 軸が対数となる片対数グラフでは式(1)~式(4)の関数は図16のように描かれる。
軸が対数となる片対数グラフでは式(1)~式(4)の関数は図16のように描かれる。
線形関数の式(1)を変形する。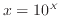 を代入し変形する。
を代入し変形する。
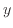 と
と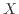 は指数関数に近い形となり、図16の線形関数を表す黒線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
は指数関数に近い形となり、図16の線形関数を表す黒線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
指数関数の式(2)を変形する。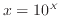 を代入し変形する。
を代入し変形する。
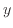 と
と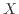 は指数関数となり、図16の指数関数を表す青線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
は指数関数となり、図16の指数関数を表す青線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
対数関数の式(3)を変形する。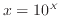 を代入し変形する。
を代入し変形する。
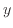 と
と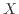 は線形関数となり、図16では対数関数を表す緑線は直線として描かれる。定数
は線形関数となり、図16では対数関数を表す緑線は直線として描かれる。定数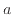 、
、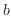 で表される対数関数を同様に変形する。
で表される対数関数を同様に変形する。
このようにグラフの傾きが
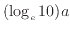 、切片がbとなる(表1)。グラフから読みとった傾きと切片から元の関数の
、切片がbとなる(表1)。グラフから読みとった傾きと切片から元の関数の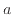 と
と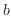 を求めることができる。
を求めることができる。
べき関数の式(4)を変形する。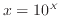 を代入し変形する。
を代入し変形する。
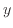 と
と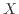 は指数関数となり、図16のべき関数を表す赤線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
は指数関数となり、図16のべき関数を表す赤線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
 軸、
軸、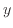 軸共に対数となる両対数グラフでは式(1)~式(4)の関数は図17のように描かれる。
軸共に対数となる両対数グラフでは式(1)~式(4)の関数は図17のように描かれる。
線形関数の式(1)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
図17で線形関数は黒線に示すようにやや下に凸の曲線になっている。
指数関数の式(2)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
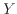 と
と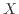 は指数関数に近い形となり、図17の指数関数を表す青線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
は指数関数に近い形となり、図17の指数関数を表す青線は線形-線形グラフ(図14)の指数関数(青線)と近い下に凸の曲線になっている。
対数関数の式(3)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
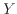 と
と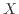 は対数関数に近い形となり、図17の対数関数を表す緑線は線形-線形グラフ(図14)の対数関数(緑線)と近い下に凸の曲線になっている。
は対数関数に近い形となり、図17の対数関数を表す緑線は線形-線形グラフ(図14)の対数関数(緑線)と近い下に凸の曲線になっている。
べき関数の式(4)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
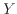 と
と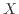 は線形関数となり、図17でべき関数は赤線に示すように直線で描かれる。定数
は線形関数となり、図17でべき関数は赤線に示すように直線で描かれる。定数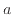 、
、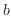 で表したべき関数を同様に変形する。
で表したべき関数を同様に変形する。
グラフの傾きが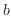 、切片が
、切片が
 となる(表1)。この読みとった傾きと切片から元の関数の
となる(表1)。この読みとった傾きと切片から元の関数の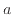 と
と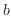 が計算できる。
が計算できる。
<戻る: 3.1 対数グラフでの見え方の違い>
<次へ: A..2 対数グラフでの変化の詳細計算>
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。
![]() 、
、![]() に対して10の対数を取った次式で表される
に対して10の対数を取った次式で表される![]() 、
、![]() との関係が表される。
との関係が表される。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し変形する。
を代入し変形する。
![]() を代入し変形する。
を代入し変形する。
![]() を代入し変形する。
を代入し変形する。
![]() を代入し変形する。
を代入し変形する。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。