<戻る: A..1 詳細な計算>
「3 対数グラフでの変化」で示したそれぞれの対数グラフで色々な関数がどのように描かれるか、の詳細計算を示す。測定した実験データを処理することを想定し測定値が一定量ずれていた場合に、それがどのようにグラフに反映されるかも見てみる。
線形-対数グラフで直線で表された次の指数関数の式を基本とする。
 方向に10ずらした式(6)、
方向に10ずらした式(6)、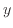 方向に2000ずらした式(7)、定数をそれぞれ変えた式(8)と式(9)でグラフがどう変わるか図18、図19に示す。
方向に2000ずらした式(7)、定数をそれぞれ変えた式(8)と式(9)でグラフがどう変わるか図18、図19に示す。
式(6)に先ほどと同様に、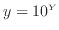 を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
図19に示すように直線となる。表1に示すように元の関数と切片が異なる
4。
式(7)に先ほどと同様に、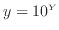 を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
図19に示すように が大きな値の領域では直線に近くなるが
が大きな値の領域では直線に近くなるが が0に近い領域では曲線となる。
が0に近い領域では曲線となる。
式(8)に先ほどと同様に、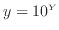 を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
対数グラフでは表1に示すように元の関数に比べ切片が増え図19に示すような直線となる。
式(9)に先ほどと同様に、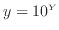 を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
対数グラフでは表1に示すように元の関数に比べ傾きが大きくなり図19に示すような直線となる。
指数関数は片対数グラフにおいて、関数中の定数が変わった場合や 方向にずれた場合では直線となるが、元の関数が
方向にずれた場合では直線となるが、元の関数が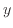 方向にずれると直線とならない。
方向にずれると直線とならない。
対数-対数グラフで直線で表された次のべき関数の式を基本とする。
 方向に10ずらした式(10)、
方向に10ずらした式(10)、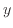 方向に20ずらした式(11)、定数をそれぞれ変えた式(12)と式(13)がどう変わるか図20、図21に示す。
方向に20ずらした式(11)、定数をそれぞれ変えた式(12)と式(13)がどう変わるか図20、図21に示す。
式(10)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
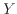 と
と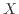 は線形関数にはならず、図21でも直線ではなく上に凸な曲線になっている。しかし
は線形関数にはならず、図21でも直線ではなく上に凸な曲線になっている。しかし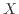 が大きくなるにつれて式4の直線に近づいていく。
が大きくなるにつれて式4の直線に近づいていく。 方向にゼロ点がずれると
方向にゼロ点がずれると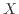 が小さな領域では直線とならず、
が小さな領域では直線とならず、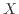 が大きくなるにつれて直線に近づくことが分かる。
が大きくなるにつれて直線に近づくことが分かる。
式(11)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
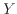 と
と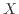 は線形関数にはならず、図21でも直線ではなく下に凸な曲線になっている。しかし式(10)と同様に
は線形関数にはならず、図21でも直線ではなく下に凸な曲線になっている。しかし式(10)と同様に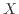 が大きくなるにつれて式4の直線に近づいていく。
が大きくなるにつれて式4の直線に近づいていく。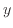 方向にゼロ点がずれた場合でも
方向にゼロ点がずれた場合でも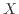 が小さな領域では直線とならず、
が小さな領域では直線とならず、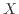 が大きくなるにつれて直線に近づく。
が大きくなるにつれて直線に近づく。
式(12)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
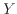 と
と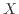 は線形の関係となり、両対数グラフ(図21)でも直線となる。表1に示すように
は線形の関係となり、両対数グラフ(図21)でも直線となる。表1に示すように の係数が変わると切片が変わる。
の係数が変わると切片が変わる。
式(13)を変形する。
 を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
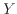 と
と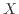 は線形の関係となり、両対数グラフ(図21)でも直線となる。表1に示すように
は線形の関係となり、両対数グラフ(図21)でも直線となる。表1に示すように の指数が変わると傾きが変わる。
の指数が変わると傾きが変わる。
べき関数は両対数グラフで、定数が変わっても直線で表されるが、 方向や
方向や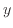 方向にずれた場合には値の小さな領域で直線から外れる。
方向にずれた場合には値の小さな領域で直線から外れる。
対数については「指数・対数のはなし?異世界数学への旅案内」[1]を読むことをお勧めする。対数のおもしろさを知ることができる。
脚注
- ...tab-Functionsに示すように元の関数と切片が異なる
4
- 関数を変形する。
このように 方向にグラフがずれた場合も変形すれば係数の値が変わった場合と同じであることが分かる。
方向にグラフがずれた場合も変形すれば係数の値が変わった場合と同じであることが分かる。
- 1
- 森 毅, 指数・対数のはなし?異世界数学への旅案内, 東京図書, 2006.
<戻る: A..1 詳細な計算>
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版およびpdf版はhttp://camelllia.netで公開している。
![]() を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
![]() を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
![]() を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
![]() を代入し両辺の10の対数をとる。
を代入し両辺の10の対数をとる。
![]() 方向にずれた場合では直線となるが、元の関数が
方向にずれた場合では直線となるが、元の関数が![]() 方向にずれると直線とならない。
方向にずれると直線とならない。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() を代入し、両辺の10の対数を取る。
を代入し、両辺の10の対数を取る。
![]() 方向や
方向や![]() 方向にずれた場合には値の小さな領域で直線から外れる。
方向にずれた場合には値の小さな領域で直線から外れる。