• 学問 -top-

1.4.5 熱機関

わかりやすい熱機関の例として、一つの過程で熱と仕事どちらかだけのやりとりとなる過程で構成されたサイクルを考える。系の体積を変化させず仕事のやりとりなしで外部と熱のみのやりとりをする等積加熱・冷却過程と、系と外部で熱のやりとりをせず体積を変化させ外部と仕事のみのやりとりをする断熱膨張・圧縮過程による熱機関を考える。先を塞いだ注射器やピストンをイメージして、図1.3のようなサイクルを考えよう。図1.3の状態1からピストンを動かないように固定し、低温の熱源の中に入れる（例えば冷たい水の中）。ピストンから冷たい水に熱が伝わり、等積冷却過程でピストン内部の温度が下がる（状態2）。冷たい水からピストンを取り出し熱が伝わらないようにして、ピストンをさらに押し断熱圧縮過程で体積を小さくする（状態3）。次はピストンを固定し温かいお湯の中にピストンを入れ等積加熱過程で変化させる（状態4）。お湯からピストンを取り出し、元の状態に戻るまで断熱膨張過程でピストンを膨張させる（状態1）。元の状態に戻り一連の過程がサイクルとなる。

図 1.3: ピストンでのサイクル

サイクルでは周囲と熱と仕事をやりとりする。それぞれの過程では以下のことが起こっている。

1→2 冷却され熱が周囲に伝わる、内部の圧力が低下（等積冷却過程）

2→3 圧縮され周囲から仕事をされる、体積が減少（断熱圧縮過程）

3→4 加熱され熱が周囲から伝わる、内部の圧力が上昇（等積加熱過程）

4→1 膨張し周囲に仕事をする、体積が増加（断熱膨張過程）

冷却や加熱をされると、圧力が変化し、断熱変化で体積が変化することにより周囲と仕事のやりとりをする。圧力の変化の概略は図1.4のようになる（圧力変化の傾きは例として示したもので、過程によって異なることもある）。図1.5に温度変化の概略を示す（温度変化の傾きは例として示したものである）。断熱圧縮時には温度は上昇し、断熱膨張時には温度は低下する。冷却の後の2→3の過程では、体積が減少することで仕事をされる。加熱の後の4→1の過程では、体積が増加し周囲に仕事をしている。体積増加の際の仕事については付録B.1（p.）に詳細を記した。

図 1.4: ピストンでのサイクルの圧力変化

仕事$W$ [J]は圧力$P$ [Pa]と微小体積変化$d V$ [m$^3$ ]の積分により

$$W = \int P d V$$

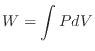
で表される ^1.6。 状態2から状態3と状態4から状態1での体積の変化量は同じであるので、仕事の大きさは圧力によって決まる。図1.4から、状態2から状態3の平均圧力より、状態4から状態1の平均圧力が大きいことが分かる。そのため、積分して得られる仕事も大きくなり、以下の式が得られる。状態2から状態3では仕事をされるため正の値、状態4から状態1では仕事をするため負の値となる。そこで、絶対値をとり大きさを比較する。

$$\left \vert \int^3_2 P dV \right \vert < \left \vert \int^1_4 P dV \right \vert$$

$$\vert W_{23} \vert < \vert W_{41} \vert$$ (1.6)

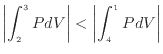
状態2から状態3では周囲から仕事をされ、状態4から状態1では周囲に仕事をしている。このことからこのサイクルでは $\vert W_{41} \vert - \vert W_{23} \vert$ の仕事を周囲にしている^1.7ことが分かる。また、状態3から状態4で周囲（熱源3-4）から熱を受け取り、状態1から状態2で周囲（熱源1-2）に熱を与えている。図1.5の温度変化の概略に示すように、周囲の温度は状態3から状態4の熱源3-4が状態1から状態2の熱源1-2よりも高い。このことから、このサイクルは高温の熱源3-4から熱を受け取り、低温の熱源1-2へ熱を与えている。

図 1.5: ピストンでのサイクルの温度変化

状態1から再度状態1へ戻るとき、内部エネルギーの値は等しく変化はゼロであるので、エネルギーの保存から以下の式が成り立つ。

$$\Delta U = 0 = Q_{12} + W_{23} + Q_{34} + W_{41}$$

$$W_{23} + Q_{34} = - W_{41} - Q_{12}$$

仕事の大きさの関係の式(1.6) p. と上式から、熱の大きさの関係を求める。状態1から状態2では外部に熱を伝えるため負の値となり、状態3から状態4では外部から熱を受け取るため正の値となる。そのため絶対値をとり大きさを比較すると、以下の式が成り立つ。。

$$\vert Q_{34} \vert > \vert Q_{12} \vert$$

低温熱源へ渡す熱の大きさよりも、高温熱源から受け取る熱の大きさのほうが大きい。以上から、高温熱源から熱を受け取り、一部を仕事に変換し外部へ取り出し、高温熱源から受け取った熱より少ない残りの熱を低温熱源へ渡している。すなわち、熱機関として動作していることがわかる。

実際に世の中で使われている熱機関として火力発電所や原子力発電所がある。発電所のサイクルは閉じた系ではないが、同じように考えられる。発電所の多くでは系の中の物質に水を用いている。発電所と図1.3のサイクルの対応は以下のようになっている。

1→2 冷却され熱が周囲に伝わる、内部の圧力が低下 : 復水器（海水で冷却）

2→3 圧縮され周囲から仕事をされる、体積が減少 : ポンプ（水を循環させる）

3→4 加熱され熱が周囲から伝わる、内部の圧力が上昇 : ボイラー（燃焼や核反応で水を沸騰させる）

4→1 膨張し周囲に仕事をする、体積が増加 : 蒸気タービン（発電機へとつながっており電気を発生させる）

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。