...
仕事は、ある物体から別の物体へ力が作用した際に伝わるエネルギーである。熱機関において、外部へされた仕事は運動エネルギーへと変換されることが多い1.1
仕事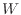 [J]をされた質量
[J]をされた質量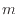 [kg]の速度
[kg]の速度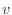 [m/s]で運動している物体の運動エネルギーの変化を示す。力
[m/s]で運動している物体の運動エネルギーの変化を示す。力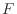 [N]は運動量の微小時間変化
[N]は運動量の微小時間変化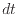 [s]により次式で定義される。通常、質量
[s]により次式で定義される。通常、質量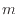 は一定と考えられるので、
は一定と考えられるので、
微小幅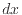 [m]の間、力を加えたときの仕事
[m]の間、力を加えたときの仕事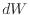 [J]は
[J]は
ここで、
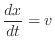 なので、
なので、
仕事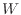 が状態0
から状態
が状態0
から状態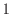 まで作用するときに、その区間で積分すると、
まで作用するときに、その区間で積分すると、
この
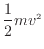 が運動エネルギーである。仕事をされることにより物体の運動エネルギーは増加する。
が運動エネルギーである。仕事をされることにより物体の運動エネルギーは増加する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J](顕熱微小変化量)は、等積比熱
1.2
等積比熱とは体積の変化しない状態で単位質量の物体を単位温度上昇させるのに必要なエネルギー量である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
熱力学において、考える対象の領域を“系”と呼ぶ。その中でも外部と物質の出入りがないが熱や仕事のやりとりはある系を“閉じた系”という1.3
外部と物質の出入りがなく熱や仕事のやりとりもない系を“孤立系”という。外部と物質の出入りも熱や仕事のやりとりもある系を“開いた系”という。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... を考える1.4
熱力学的な取り扱いをする際、系の状態は熱力学的平衡が成り立っている必要がある。しかし、ある平衡状態から次の平衡状態へ変化する間の過程では必ずしも常に平衡状態が維持されている必要はない。変化中の非平衡の系を扱うことはできないが、変化前の平衡状態と変化後の平衡状態の系の変化については取り扱うことが出来る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fig-PistonWorkHeatのようにピストン形状の系を考える。可動壁には壁を支える支持棒がついており、系の圧力と釣り合うように支持棒に力を加える。仕事のやりとりのない過程では、可動壁を固定して動かないようにする。通常周囲の空気などにより大気圧が作用するが、ここでは大気圧のような圧力は考慮せず支持棒のみに力がかかっていると考える
1.5
周囲の圧力と支持棒の力の和と系の圧力による力が釣り合うように支持棒に力を加えるため、周囲の圧力が異なっても支持棒の力が変わるだけで、周囲の圧力の変化による系のする仕事への影響はない。系の圧力と周囲の圧力、支持棒に加える力については付録B.1(p. ![[*]](crossref.png) )に詳細を示す。系は支持棒と周囲に対して仕事をするため、“周囲との仕事のやりとり”ではなく、“周囲と支持棒との仕事のやりとり”、と表現するべきであるが、ここでは“周囲との仕事のやりとり”に系のした(された)仕事すべてを含めることとする。
)に詳細を示す。系は支持棒と周囲に対して仕事をするため、“周囲との仕事のやりとり”ではなく、“周囲と支持棒との仕事のやりとり”、と表現するべきであるが、ここでは“周囲との仕事のやりとり”に系のした(された)仕事すべてを含めることとする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
で表される1.6
体積が変化し、外部と仕事のやりとりのある状態2から状態3と状態4から状態1での仕事の大きさを考える。
ピストンにかかる力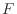 [N]は圧力
[N]は圧力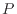 [Pa]とピストンの断面積
[Pa]とピストンの断面積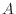 [m
[m ]により
]により
と表される。力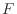 [N]を加え微小な距離
[N]を加え微小な距離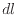 [m]動かす際の、微小な仕事
[m]動かす際の、微小な仕事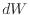 [J]は
[J]は
と表される。ピストンを微小に動かした体積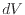 [m
[m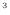 ]は、ピストンの断面積
]は、ピストンの断面積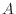 [m
[m ]と、微小な移動距離(ピストンを動かした距離)
]と、微小な移動距離(ピストンを動かした距離)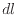 [m]から、
[m]から、
で表されるので、
となる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... の仕事を周囲にしている1.7
絶対値を外すと
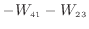
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...の仕事1.8
絶対値を外すと
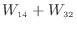
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 膨張弁(仕事は取り出さず、粘性消散1.9
流れで渦が発生し徐々に小さな渦となり、粘性により渦の運動エネルギーが熱に変換される
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
と定義される1.10
高温熱源側を利用する場合はヒートポンプと呼ばれる。また、低温熱源側を利用する場合は冷凍機と呼ばれ、効率の分子は低温熱源とやりとりする熱量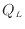 となる。またヒートポンプや冷凍機の効率はCOP(Coefficient of Performance)とも呼ばれる。
となる。またヒートポンプや冷凍機の効率はCOP(Coefficient of Performance)とも呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
効率の高い可逆サイクルAを熱機関として、可逆サイクルBをヒートポンプとして、仕事の大きさが同じになるように動作させ1.11
それぞれのサイクルの仕事の大きさが違う場合は、同じサイクルを複数個まとめて動作させて、それぞれの数を調整し、総計で同じ仕事となるように調整する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...を、同じ大きさになるよう
1.12
伝わる熱の大きさを同じにするように、サイクル2とサイクル3を複数個一緒に動作させ、それぞれのサイクルの数を調整する。複数のサイクルを一つのサイクルとして考えれば、伝わる熱の大きさを等しくすることが出来る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... で示した熱力学的平衡の熱平衡、力学平衡、相平衡、化学平衡のうち、閉じた系と周囲との間で物質の直接接触や物質の移動がないので、系と周囲の関係で相平衡、化学平衡については考える必要がない1.13
また断熱変化では熱平衡を、等積変化では力学平衡を考える必要がない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...も前後の状態で決まる1.14
準静過程でない場合は仕事が前後の状態で決まらないため、熱量もどの程度の大きさとなるか前後の状態だけでは分からない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...sec-2ndLaw)に定義されるように低温から高温へ他に影響を及ぼさず熱を伝えることはできない。温度差がある物体間で熱が伝わる場合は必ず不可逆となる(温度の高い物体から低い物体に熱は伝わるが、温度の低い物体から高い物体へは熱は伝わらない)。熱が発生する場合も不可逆である。例えば、系の内部では運動エネルギーが粘性消散2.1
流れで渦が発生し徐々に小さな渦となり、粘性により渦の運動エネルギーが熱に変換される
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...実際に起こる現象は全て不可逆であり、可逆の現象は理想化された現象である。可逆の現象は時間がそのまま進んだ場合の変化を逆向きにした場合の変化も起こすことができる
A.1
現象をカメラで動画を撮って、そのまま再生した場合と逆再生をした場合にどちらの映像も現象に異常がない場合が可逆の現象である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...は任意の有限の温度差とする。熱伝導での熱の伝わりを考えると、熱伝導の式(フーリエの法則B.1
詳細は伝熱のテキスト[7][8]を参照すること
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...[J]は熱伝導で伝わり、熱伝導の式(フーリエの法則)により次のようになる(壁の中の温度分布は線形と仮定する)B.2
詳細は伝熱のテキスト[7][8]を参照すること
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...また、系の内部での平衡の条件を考える。過程において系の内部で力学平衡が維持できない条件として、内部で圧力分布があり流れが起きる状態があげられる。内部での熱平衡が維持できない条件では温度が一定ではなく温度分布ができるため平衡ではない。また、等温変化において圧力変化での圧縮や膨張による温度変化が、壁からの伝熱による温度変化よりも早ければ、内部の温度が周囲の等温環境の温度とは異なる。圧力と温度が周囲と同じ場合と異なるため、仕事が減りやりとりする熱が増える。また、ピストンの移動速度によりやりとりする仕事が変化することも考えられる
B.3
系の内部分子の速度に対してピストンの速度が大きく速いとき、体積増加では壁が遠ざかることから受ける圧力が小さくなり、取り出せる仕事が減る。体積減少の過程では相対速度が増え、必要な仕事が増える。速度としては音速のオーダーであり、圧力波が発生すると思われる。通常、移動速度により変化する仕事の量は測定できないほど小さい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...sec-LocalThermodynamicEquilibrium)が成り立っていれば、実際の現象においても断熱変化は可逆過程となりうる(系の内部で流れによる粘性消散B.4
流れで渦が発生し徐々に小さな渦となり、粘性により運動エネルギーが熱に変換される
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
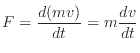
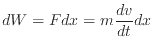
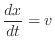 なので、
なので、
![]() が状態0
から状態
が状態0
から状態![]() まで作用するときに、その区間で積分すると、
まで作用するときに、その区間で積分すると、
![$\displaystyle W = \int_0^1 dW = \int_0^1 F dx = \int_0^1 m v dv = m \int_0^1 v ...
...m \biggl[\frac{1}{2} v^2 \biggr]_0^1 = \frac{1}{2} mv_1^2 - \frac{1}{2} mv_0^2
$](img17.png)
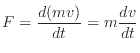
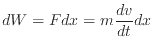
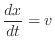 なので、
なので、
![]() が状態0
から状態
が状態0
から状態![]() まで作用するときに、その区間で積分すると、
まで作用するときに、その区間で積分すると、
![$\displaystyle W = \int_0^1 dW = \int_0^1 F dx = \int_0^1 m v dv = m \int_0^1 v ...
...m \biggl[\frac{1}{2} v^2 \biggr]_0^1 = \frac{1}{2} mv_1^2 - \frac{1}{2} mv_0^2
$](img17.png)
![[*]](crossref.png) )に詳細を示す。系は支持棒と周囲に対して仕事をするため、“周囲との仕事のやりとり”ではなく、“周囲と支持棒との仕事のやりとり”、と表現するべきであるが、ここでは“周囲との仕事のやりとり”に系のした(された)仕事すべてを含めることとする。
)に詳細を示す。系は支持棒と周囲に対して仕事をするため、“周囲との仕事のやりとり”ではなく、“周囲と支持棒との仕事のやりとり”、と表現するべきであるが、ここでは“周囲との仕事のやりとり”に系のした(された)仕事すべてを含めることとする。
![]() [N]は圧力
[N]は圧力![]() [Pa]とピストンの断面積
[Pa]とピストンの断面積![]() [m
[m![]() ]により
]により