• 学問 -top-

1.5.1 可逆サイクルの効率

ここでは可逆サイクルの効率（仕事と熱の比）はどんな可逆サイクルでも常に等しくなることを示す。 可逆サイクルAと可逆サイクルBを並べて同じ二つの熱源間で動作させる。可逆サイクルAの熱機関としての効率 $\epsilon_{E, A}$ が、可逆サイクルBの熱機関としての効率 $\epsilon_{E, B}$ よりも高いと仮定する（図1.10-1）。

$$\epsilon_{E, A} > \epsilon_{E, B}$$ (1.12)

効率の高い可逆サイクルAを熱機関として、可逆サイクルBをヒートポンプとして、仕事の大きさが同じになるように動作させ^1.11（図1.10-2）、熱機関で取り出した仕事でヒートポンプを動作させる（図1.10-3）。

図 1.10: 可逆サイクルの比較

式(1.9)と式(1.12)から

$$\frac{ \vert W_A \vert }{ \vert Q_{A, H} \vert } > \frac{ \vert W_B \vert }{ \vert Q_{B, H} \vert }$$

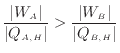
ここで仕事が同じとなるように動作させているので $\vert W_A \vert = \vert W_B \vert$ となり、次式が成り立つ。

$$\vert Q_{A, H} \vert < \vert Q_{B, H} \vert$$ (1.13)

ここで、上式とサイクルにおけるエネルギー保存の式(1.8)（p. ）と式(1.10)（p. ）より、

$$\vert Q_{A, L} \vert + \vert W_A \vert < \vert Q_{B, L} \vert + \vert W_B \vert$$

ここで、仕事の大きさが同じになるように動作させている( $\vert W_A \vert = \vert W_B \vert$ )ので、次式の関係となる。

$$\vert Q_{A, L} \vert < \vert Q_{B, L} \vert$$ (1.14)

この可逆サイクルである熱機関Aと可逆サイクルであるヒートポンプBでは、仕事は熱機関AからヒートポンプBへするため、周囲との仕事のやりとりはない。そのため図1.10-4のようにまとめて一つのサイクルとして考えることができる。高温熱源では、式(1.13)より $\vert Q_{B, H} \vert - \vert Q_{A, H} \vert > 0$ となり、ヒートポンプとして動作している可逆サイクルBの熱$Q_{B, H}$ が大きく、まとめたサイクルから高温熱源へ熱を伝えている。低温熱源では、式(1.14)より $\vert Q_{B, L} \vert - \vert Q_{A, L} \vert > 0$ となり、ヒートポンプとして動作している可逆サイクルBの熱$Q_{B, L}$ が大きく、まとめたサイクルで低温熱源から熱を受け取っている。このように、二つのサイクルを合わせた全体で見ると、低温熱源から熱を受けとり、高温熱源へ熱を渡し、他に何の変化も残していないことになる。これは熱力学第二法則のクラウジウスの原理（1.3節、p. ）に反する。よって、可逆サイクルBの熱機関としての効率が可逆サイクルAの熱機関としての効率よりも高くなることはありえない。

可逆サイクルAの熱機関としての効率が可逆サイクルBよりも低いとした場合も、AとBを入れ替えて考え、可逆サイクルBを熱機関、可逆サイクルAをヒートポンプとして動作させると、同様に低温熱源から高温熱源に熱を伝え、他になにも変化を残さないことになる。よって、同様にクラウジウスの原理から、可逆サイクルAの熱機関としての効率が可逆サイクルBの熱機関としての効率よりも高くなることはありえない。

よって、同じ二つの熱源間で動作する可逆サイクルは必ず同じ効率となる。

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。