• 学問 -top-

1.4.7 サイクルの効率

熱機関とヒートポンプの効率を定義しよう。図1.9に二つの熱源で動作する熱機関とヒートポンプの概要を示す。熱と仕事はサイクルへ入るものを正、出るものを負としている。サイクルでは内部エネルギーの変化$\Delta U$ がゼロ（式(1.5)、p. ）であるので、熱機関では第一法則（式(1.4)、p. ）より熱機関の高温熱源から受け取る熱$Q_{E, H}$ （正の値）と低温熱源に移す熱$Q_{E, L}$ （負の値）、得られる仕事$W_E$ （負の値）（得られる仕事の大きさは1.4.5節の $\vert W_{41} \vert - \vert W_{23} \vert$ にあたる）の関係は

$$W_E + Q_{E, H} + Q_{E, L} = 0$$

絶対値で表すと以下のようになる。

$$\vert W_E \vert = \vert Q_{E, H} \vert - \vert Q_{E, L} \vert$$ (1.8)

図 1.9: 熱機関とヒートポンプ

熱機関では仕事を取り出すことが目的であるので、少ない高温熱源からの熱で多くの仕事に変換出来ると効率がよいといえる。そこで、熱機関の効率 $\epsilon_E$ は式(1.8)より

$$\epsilon_E = \frac{ \vert W_E \vert }{ \vert Q_{E, H} \vert } = \frac{ \vert Q_{E, H} \vert - \vert Q_{E, L} \vert }{ \vert Q_{E, H} \vert }$$ (1.9)

絶対値を外すと

$$\epsilon_E = - \frac{ W_E }{ Q_{E, H} } = \frac{ Q_{E, H} + Q_{E, L} }{ Q_{E, H} }$$

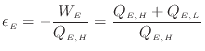
と定義される。

ヒートポンプでは第一法則（式(1.4)、p. ）より低温熱源から受け取る熱$Q_{P, L}$ （正の値）と高温熱源へ移す熱$Q_{P, H}$ （負の値）、必要な仕事$W_P$ （正の値）（必要な仕事の大きさは1.4.6節の $\vert W_{14}\vert - \vert W_{32}\vert$ にあたる）の関係は

$$W_P + Q_{P, H} + Q_{P, L} = 0$$

絶対値により次のように表される。

$$\vert W_P \vert = \vert Q_{P, H} \vert - \vert Q_{P, L} \vert$$ (1.10)

ヒートポンプでは低温熱源から高温熱源へ熱を伝えるのが目的であるので、少ない仕事で多くの熱を移せると効率がよいといえる。そこで、ヒートポンプの効率 $\epsilon_P$ は

$$\epsilon_P = \frac{ \vert Q_{P, H} \vert }{ \vert W_P \vert } = \frac{ \vert Q_{P, H} \vert }{ \vert Q_{P, H} \vert - \vert Q_{P, L} \vert }$$ (1.11)

絶対値を外すと

$$\epsilon_P = - \frac{ Q_{P, H} }{ W_P } = \frac{ Q_{P, H} }{ Q_{P, H} + Q_{P, L} } \nonumber$$

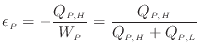
と定義される^1.10。

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。