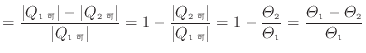


Next: 1.4.8 まとめ
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.6 可逆熱機関(可逆ヒートポンプ)での熱の比
1.4.7 可逆熱機関(可逆ヒートポンプ)と温度
式(1.31)の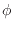 は単一の温度の関数である。この式(1.31)の関係から温度を定義する。次の式のように関数
は単一の温度の関数である。この式(1.31)の関係から温度を定義する。次の式のように関数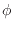 をそのまま定義したものが熱力学的温度(絶対温度)
をそのまま定義したものが熱力学的温度(絶対温度)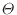 で単位は[K](ケルビン)である[2]1.18。
で単位は[K](ケルビン)である[2]1.18。
また日常使われる摂氏温度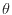 [℃]は国際的にSI(国際単位系)の組立単位として絶対温度
[℃]は国際的にSI(国際単位系)の組立単位として絶対温度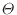 [K]により次式で定義されている[3]。
[K]により次式で定義されている[3]。
よって関数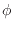 と摂氏温度
と摂氏温度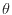 [℃]の関係は次式で表される。
[℃]の関係は次式で表される。
この熱力学的温度で表現すると、温度
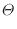 1
[K]と温度
1
[K]と温度
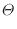 2
[K]の二つの熱源で動作する可逆熱機関の熱源とやりとりする熱量
2
[K]の二つの熱源で動作する可逆熱機関の熱源とやりとりする熱量
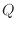 1
[J]と熱量
1
[J]と熱量
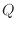 2
[J]の関係は次のように熱力学的温度(絶対温度)の比で表される。
2
[J]の関係は次のように熱力学的温度(絶対温度)の比で表される。
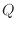 1
[J]と
1
[J]と
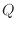 2
[J]は熱機関(ヒートポンプ)に対し入る向きと出る向きと伝わる方向が逆であり、符号が逆となるので絶対値を外して変形し次式となる。
2
[J]は熱機関(ヒートポンプ)に対し入る向きと出る向きと伝わる方向が逆であり、符号が逆となるので絶対値を外して変形し次式となる。
式(1.10)
 と式(1.32)より、温度
と式(1.32)より、温度
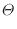 1
[K]の熱源と温度
1
[K]の熱源と温度
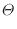 2
[K]の熱源(
2
[K]の熱源(
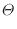 1
1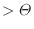 2
)で動作する可逆熱機関の効率は次式(1.34)で表される。
2
)で動作する可逆熱機関の効率は次式(1.34)で表される。



Next: 1.4.8 まとめ
Up: 1.4 可逆熱機関(可逆ヒートポンプ)
Previous: 1.4.6 可逆熱機関(可逆ヒートポンプ)での熱の比
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() 1
[K]と温度
1
[K]と温度
![]() 2
[K]の二つの熱源で動作する可逆熱機関の熱源とやりとりする熱量
2
[K]の二つの熱源で動作する可逆熱機関の熱源とやりとりする熱量
![]() 1
[J]と熱量
1
[J]と熱量
![]() 2
[J]の関係は次のように熱力学的温度(絶対温度)の比で表される。
2
[J]の関係は次のように熱力学的温度(絶対温度)の比で表される。