3.1 熱力学第零法則
熱力学第零法則とは「系Aと系Bが熱平衡であり、系Aと系Cも熱平衡であれば、系Bと系Cも熱平衡である」ことを示す法則である。少し意味がとりづらいと思うが、この法則は温度の測定に必要不可欠な法則である。法則中の系Aが温度計の役割を果たす。
3.1.1 温度の比較
温度の比較は長さや質量と比べると非常に難しい。 温度の比較をし、測定するための約束事を決めたのが熱力学第零法則である。 測定することは基準と比較することである。図3.1のように、長さであれば定規のような基準となるものと目で見て比較して長さを測れる。質量であれば基準となるおもりと天秤で比べ、釣り合ったおもりで質量が量れる。では、温度はどのように比較をしたらよいだろうか。
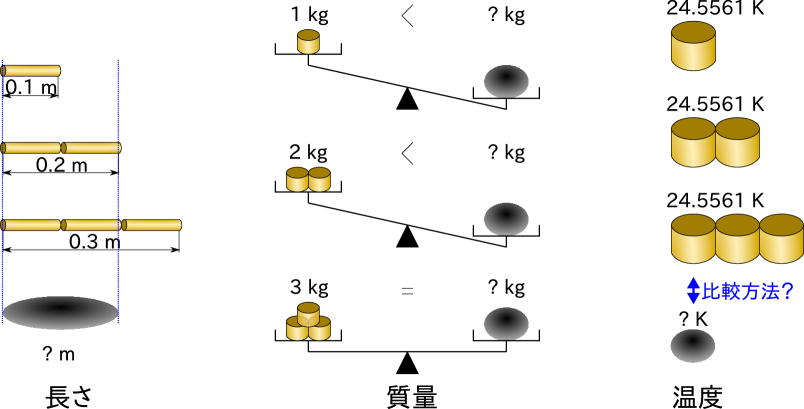
温度の比較の難しさの一つは基準を複数持ってきても、基準となる値が増えないことである。図3.1のように、長さであれば、0.1 mの基準が2つあれば0.2 m、3つあれば0.3 mを測ることが出来る。質量も秤を使うことで1 kgのおもりが2個あれば2 kg、3個あれば3 kgを測ることが出来る。しかし、温度の場合はそうではない。例えば国際温度目盛(ITS-90)[23]で基準温度として使われている24.5561 Kの三重点 111三重点とは三相(例えば気相・液相・固相)が共存する状態である。ギブスの相律により三相が共存する状態では温度と圧力が変化しない。二相状態では温度と圧力どちらかのみ変化できる(水の沸点は圧力が決まれば温度が決まり、沸騰する状態は点ではなく線で表される)。単相状態ではどんな温度、圧力の状態でもとれる。 の状態のヘリウムは1つでも2つでも同じ温度24.5561 Kであり、長さや質量のように2個あれば2倍の温度が測れる訳ではない。長さや質量のように2個あれば2倍の値になるものを示量性の量、温度のように増えても変わらない強さを表すものを示強性の量と呼ぶ。
温度の比較のもう一つの難しさとして、同じ値であると判断することが簡単ではないことである。図3.1のように、長さであれば目で見て基準の長さと比べることで、精度はともかくとして同じ長さであると判断できる。また、質量であれば基準の質量と秤が釣り合えば同じ値であると判断できる。「基準の温度24.5561 Kのもの」と、「温度が不明なもの」がある場合にどのように比べたらいいだろうか。これまで示したように、熱は温度差がある際に伝わる。すなわち「基準の温度のもの」と「温度が不明なもの」の間で熱が伝わらない熱平衡の状態であれば、温度差がない、同じ温度であると判断できる。
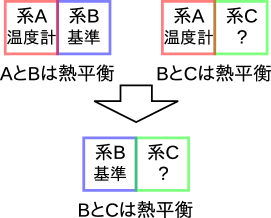
熱平衡になった状態を同じ温度とし、その熱平衡の性質を決めたのが熱力学第零法則である。基準温度となる物質をいくつか準備し、その基準に合わせて温度計のメモリをつくる。温度計(系A)と基準物質(系B)が熱平衡の状態でメモリをつくる。物体Cと温度計(系A)が熱平衡になる温度計(系A)のメモリが分かれば、熱力学第零法則から基準物質(系B)と温度を知りたい物体Cも熱平衡であるため、基準物質と比べることが可能となる(図3.2)。 熱平衡であれば温度が比較できる、つまり熱平衡にあるときのみ温度を測定することが出来るのである。熱平衡にないときは温度が測定できない。測定できない値は使えないため、温度を使うためには対象が熱平衡である必要がある。温度の測定の難しさについての詳細を付録のC.1節に記した。
3.1.2 局所熱力学的平衡
局所熱力学的平衡を考えることで、完全に熱平衡となった系でなくても温度を扱うことができる。温度を扱うためには熱平衡でなくてはならないが、熱平衡は断熱され十分に時間が経過した後の温度が一定の状態であり、現実には周囲の状況は刻々と変わりその影響を受けるため温度が一定となることはありえない。ほぼ全ての系が非平衡であり、熱のやりとりがある熱機関やヒートポンプも非平衡状態である。そのため、熱平衡ではないほとんどの場合で温度を扱うことができないこととなってしまう。しかし、温度を扱えないと困るため、局所的に熱平衡である、と考える。 実際に私たちが温度を日常的に使い測定している場合には局所的に熱平衡であるとして測定をしている。
局所熱力学的平衡では系を非常に小さくとり局所的には温度や圧力の分布が一様で熱力学的平衡が成り立っていると考える 222 この局所熱力学的平衡はほとんどの現実的な状況において成り立つと考えられ、統計熱力学的には分子数とエネルギーの関係がボルツマン分布となる。連続体として扱えないような分子数が少ない場合や変化の時間が短い場合は局所熱力学的平衡が成り立たないこともある。。 例えば、1 cm3の容器内での1 msの時間で起こる状態変化は十分に局所熱力学的平衡を満足している[13]。このことから、局所熱力学的平衡が成り立つ系であれば、全体として熱力学的平衡が成り立っていない系であってもこれまでの熱力学の結果を適用できる(温度などを使える)。 より詳しい内容について興味があれば文献[13][7]や、ボルツマン分布については統計熱力学の参考書を参照するとよい。温度とボルツマン分布についてはAtkinsの本[3]もわかりやすい。