3.2 温度

温度についてより詳しく見ていく。

3.2.1 温度の基準

温度の基準となる温度計はどのように作ればいいだろうか。基準としやすい温度として、水は約100℃で沸騰する。大気圧下で水が沸騰しているときは常に約100℃である。また、水が凍り始め水と氷が混ざった状態になると大気圧下では常に約0℃である。これは身の回りで簡単に実現できて、温度もほぼ一定となるため、基準としやすい（ただ水の沸騰の温度と凍結の温度は気圧や水の純度により変わるため正確な基準としにくい）。摂氏温度は初めはこの水が沸騰する温度と凍り始める温度を基準としていた。その後、圧力によらない基準点として特定の物質の三重点が用いられ、 1990年国際温度目盛(ITS-90)[23]では、ネオンの三重点24.5561 Kや水の三重点273.16 Kなどが絶対温度の基準温度として決められている。この基準温度の間の温度を決めるための方法が必要である。長さや質量と違い、温度では基準の間の値を決めることが難しい。先に示した図3.1 ${}^{\text{p.\ref{fig-TemperatureComparison}}}$ のように、長さや質量と違い複数個基準があればより長くより重く測れるわけではなく、基準がいくつあっても同じ温度にしかならない。

例えば、基準温度であるネオンの三重点24.5561 Kと水の三重点273.16 Kの物体が手元にある場合に、自分の体の温度が何度であるか知るためにはどうしたらいいだろうか。図3.1 ${}^{\text{p.\ref{fig-TemperatureComparison}}}$ のように自分の長さを測る場合には、基準となる0.1 mの物体が複数個あれば2つで0.2 m、3つで0.3 mと基準となる物体に応じた精度で長さを測ることができる。また、質量であれば、自分の質量を測る場合に基準となる1 kgの物体が複数個あれば、秤を使うことにより重量を比較しある程度の精度で質量を知ることができる。しかし、温度は強さを表す示強性状態量であるので24.5561 Kの基準が何個あっても、他の温度を測ることはできない（2つで49.1122 Kのように）。24.5561 Kの物体は何個あっても24.5561 Kのままである。

では、現在流通されている温度計はどのように温度を測っているのだろうか。よく見かける棒温度計では内部の液体（水銀や赤色の色素の入ったエタノール）が温度上昇で膨張することを利用し、体積に応じた温度を示している。メモリをつけるためにまず、沸騰する水と局所的に熱平衡とし、その時の棒温度計の指示値を100℃とする。次に氷水と局所的に熱平衡とし、そこを0℃とする。これで、二つメモリができた。しかし、その間の30℃や50℃はどのようにメモリをふればいいだろうか。この液体の体積と温度の関係は単純に温度が二倍になれば体積が二倍という変化ではなく、温度ごとに体積変化の傾向が違う。そのため、温度による体積変化を利用した棒温度計を作るには、体積と温度の関係を知る必要がある。体積と温度との関係を知るためには（温度計を作るためには）、基準となる温度の間を埋める方法が定義されている必要がある。

3.2.2 熱力学的温度

熱力学的温度（絶対温度） $\varTheta$ [K]として2.4.6節 ${}^{\text{p.\ref{sec-AbsoluteTemperature}}}$ で示したように、温度の基準の間の温度をどうとるかを決めているのが、可逆サイクルでのそれぞれの熱源とやりとりする熱量の比を示した次式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ である。

\displaystyle\frac{|Q_{\mathrm{2可}}|}{|Q_{\mathrm{1可}}|}=\frac{\varTheta_{2}}{% \varTheta_{1}}

(2.15)

この熱力学的温度とともに、よく出てくる絶対温度に理想気体温度がある。2019年に発効した国際単位系（SI）第9版から温度の基準は特定の物質の三重点の温度ではなく、ボルツマン定数により定義されるようになった[22]。ボルツマン定数と温度の関係として、ボルツマン定数 $k_{\mathrm{B}}$ とアボガドロ数 $N_{\mathrm{A}}$ の積は気体定数となる。アボガドロ数もボルツマン定数と同様に国際単位系（SI）第9版において定義とされている定数で、それぞれ $N_{\mathrm{A}}=6.022\;140\;76\times 10^{23}\;\mathrm{mol}^{-1}$ 、 $k_{\mathrm{B}}=1.380\;649\times 10^{-23}\;\mathrm{J/K}$ このことから理想気体の状態方程式が次のように表される。

\displaystyle PV=nk_{\mathrm{B}}N_{\mathrm{A}}\varTheta

(3.1)

理想気体の状態方程式での理想気体温度と熱力学的温度は同じ値を示す（付録C.2節 ${}^{\text{p.\ref{sec-IdealGasTemperature}}}$ ）。

しかし、実在しない可逆サイクルや理想気体では温度計を作るさいに使えない。そこで、温度計を作る際に比較対象となる基準を温度域ごとに実際に手に入る計測機器で定めた1990年国際温度目盛(ITS-90)[23]が今でも温度計の校正に使われている。例えば水素の三重点13.8033 Kから銀の融点1234.93 Kの間は基準点で校正された白金測温抵抗体の値で定義される。間の基準点にはネオンの三重点24.5561 K、水銀の三重点234.3156 K、水の三重点273.16 K、アルミの融点933.473 Kなどがある[23]。より詳しい内容に興味があれば、1990年国際温度目盛(ITS-90)の日本語訳の文献[23]が無料で公開されているので参照すると良い。また、日常使われる摂氏温度 $\theta$ [℃]は2.4.6節 ${}^{\text{p.\ref{sec-AbsoluteTemperature}}}$ に示したように次式で国際的にSI単位系において組立単位として定義されている[22]。

\varTheta=\theta+273.15

3.2.3 問題

1.

ある温度のわからない物体と三相状態にある水（三重点273.16 K）との間で可逆熱機関を動作せた。可逆熱機関は、物体から100 Jの熱を受け取り、水へ70 Jの熱を渡した。ある物質の温度を求めよ。
2.

基準温度の物質として三相状態にあるネオン（三重点24.5561 K）と三相状態にある水（三重点273.16 K）と二つの任意の温度の熱源間で動作できる可逆の熱機関があり、熱源と物体は熱が伝わっても温度が変わらず、伝わった熱量は正確に測定できるとする（図3.3）。この中で二つを使って物体の温度を測る方法を述べよ。

Figure 3.3: 温度の測定
3.

前問で答えた方法で100 ℃の物体を測った際の伝わる熱量の比を高温側を分母として求めよ。

3.2.4 解答

1.

可逆熱機関から水へ伝わる熱量 $Q_{\mathrm{水}}$ [J]、水の絶対温度 $\varTheta_{\mathrm{水}}$ [K]、物体に伝わる熱量 $Q_{\mathrm{物体}}$ [J]、物体の絶対温度 $\varTheta_{\mathrm{物体}}$ [K]の関係は式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ より次のように表される。

$\frac{|Q_{\mathrm{水}}|}{|Q_{\mathrm{物体}}|}=\frac{\varTheta_{\mathrm{水}}}{% \varTheta_{\mathrm{物体}}}$

求めたい物質の温度を左辺とした式に変形し値を代入する。

$\displaystyle\varTheta_{\mathrm{物体}}$ $\displaystyle=\frac{|Q_{\mathrm{物体}}|}{|Q_{\mathrm{水}}|}\varTheta_{\mathrm{水}}$

$\displaystyle=\frac{100\mathrm{J}}{70\mathrm{J}}\times 273.16\mathrm{K}$

$\displaystyle\simeq 390.23\mathrm{K}$
2.

基準温度であるネオンか水のどちらかと、温度のわからない物体間で可逆の熱機関を動作させる。ネオンと温度のわからない物体間で可逆サイクルを動作させると、可逆サイクルからネオンへ伝わる熱量 $Q_{\mathrm{ネオン}}$ [J]、物体に伝わる熱量 $Q_{\mathrm{物体}}$ [J]、物体の絶対温度 $\varTheta_{\mathrm{物体}}$ [K]の関係は式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ より次のように表される。

$\displaystyle\frac{|Q_{\mathrm{物体}}|}{|Q_{\mathrm{ネオン}}|}=\frac{\varTheta_{% \mathrm{物体}}}{24.5561\mathrm{\>K}}$

上式を変形し、物体の温度は次式で求められる。

$\varTheta_{\mathrm{物体}}=\frac{|Q_{\mathrm{物体}}|}{|Q_{\mathrm{ネオン}}|}\times 24.% 5561\mathrm{\>K}$

水を基準とした場合には次式となる。

$\varTheta_{\mathrm{物体}}=\frac{|Q_{\mathrm{物体}}|}{|Q_{\mathrm{水}}|}\times 273.1% 6\mathrm{\>K}$

伝わった熱量を測定し、その比を求めて上式に入れることで温度を求めることができる。図3.4に示すように参照する物質（水またはネオン）と可逆熱機関が温度計となり、熱量 $Q_{\mathrm{物体}}$ [J]と $Q_{\mathrm{水}}$ [J]または $Q_{\mathrm{ネオン}}$ を読み取り上式へ代入することで温度を測定できる。³³3物体と参照物質のどちらを高温側にするかは、物体の温度によって変える。

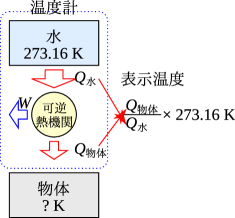Figure 3.4: 温度の測定方法
3.

前問と同様、式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ よりネオンを基準とすると次式が成り立つ。

$\frac{|Q_{\mathrm{ネオン}}|}{|Q_{\mathrm{物体}}|}=\frac{24.5561\mathrm{\>K}}{(100+2% 73.15)\mathrm{\>K}}\simeq 0.0658$

水を基準とすれば次のようになる。

$\frac{|Q_{\mathrm{水}}|}{|Q_{\mathrm{物体}}|}=\frac{273.16\mathrm{\>K}}{(100+273.% 15)\mathrm{\>K}}\simeq 0.7321$

3.1 熱力学第零法則 References 4 状態量

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。

	$\displaystyle\varTheta_{\mathrm{物体}}$	$\displaystyle=\frac{\|Q_{\mathrm{物体}}\|}{\|Q_{\mathrm{水}}\|}\varTheta_{\mathrm{水}}$
		$\displaystyle=\frac{100\mathrm{J}}{70\mathrm{J}}\times 273.16\mathrm{K}$
		$\displaystyle\simeq 390.23\mathrm{K}$