...eq-diff)で表される。入ってくる物理量はベクトルで表され、ベクトルの変化は発散2.1
ベクトル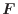 に対する発散は
に対する発散は
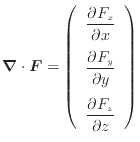 である。
である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq-govB)の“拡散による出入”で表され、運動量の拡散(粘性2.2
容器の中に粘性係数が高い流体(例えば水飴)と粘性係数が低い流体(例えば空気)で満たしその中で手を動かした時、手が流体に与えた運動量が拡散すると遠くの流体も手と一緒に動き、手は大きな力を感じる。運動量が拡散しづらい流体では近くの流体しか手と一緒に動かないので、手はあまり大きな力を感じない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.../s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3
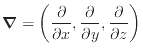
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...sec-DifferentialTerm)。変形2.4
計算は付録の式(A.2) p. ![[*]](crossref.png) 参照
参照
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...eq-press)2.5
この式中の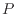 [Pa]は流体力学的圧力である。詳しくは参考文献[1]を参照のこと。
[Pa]は流体力学的圧力である。詳しくは参考文献[1]を参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
時間あたりの仕事(仕事率)は面に作用する力と速度の内積で表される2.6
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
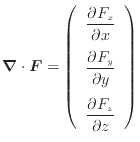 である。
である。
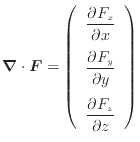 である。
である。
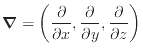
![[*]](crossref.png) 参照
参照