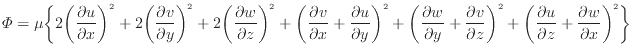


Next: 2.4.5 エネルギー保存式
Up: 2.4.4 時間あたりの仕事
Previous: 2.4.4.1 圧縮性流体(密度 [kg/m ]は変化する)
密度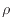 [kg/m
[kg/m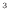 ]が一定の非圧縮性流体の場合は面に垂直な
]が一定の非圧縮性流体の場合は面に垂直な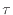 の式(2.180)
の式(2.180)
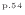 は質量保存の式(2.38)
は質量保存の式(2.38)
 p.
p.![[*]](crossref.png)
 から次式のようになる。
から次式のようになる。
 |
(2.182) |
xyz軸での出入の総和式(2.181)
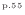 へ面に垂直な
へ面に垂直な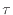 [Pa]の上式(2.183)
[Pa]の上式(2.183)
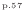 と面に平行な
と面に平行な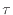 [Pa]の式(2.66)
[Pa]の式(2.66)
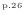 を代入すると、コントロールボリューム全体での時間あたりの仕事が次式で求められる。
を代入すると、コントロールボリューム全体での時間あたりの仕事が次式で求められる。
ここで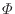 [W/m
[W/m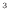 ]はエネルギー散逸関数であり次式で表される。
]はエネルギー散逸関数であり次式で表される。



Next: 2.4.5 エネルギー保存式
Up: 2.4.4 時間あたりの仕事
Previous: 2.4.4.1 圧縮性流体(密度 [kg/m ]は変化する)
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() [kg/m
[kg/m![]() ]が一定の非圧縮性流体の場合は面に垂直な
]が一定の非圧縮性流体の場合は面に垂直な![]() の式(2.180)
の式(2.180)
![]() は質量保存の式(2.38)
は質量保存の式(2.38)
![]() p.
p.![[*]](crossref.png)
![]() から次式のようになる。
から次式のようになる。