


Next: A. 付録
Up: 2.6 一般形
Previous: 2.6.0.1 圧縮性流体(密度 [kg/m ]は変化する)
- 質量保存式
- 式(2.38)
| 0 |
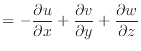 |
|
| 0 |
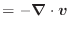 |
|
- 運動量保存式
- 式(2.92)
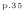
- エネルギー保存式
- 式(2.190)
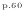
- 成分の質量保存式
- 式(2.236)
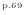
上式において物性値などの一定値(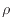 [kg/m
[kg/m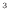 ]、
]、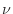 [m
[m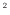 /s]、
/s]、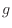 [m/s
[m/s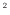 ]、
]、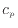 [J/(kg
[J/(kg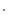 K)]、
K)]、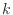 [W/(K
[W/(K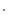 m)]、
m)]、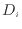 [m
[m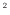 /s])を除くと未知数は
/s])を除くと未知数は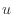 [m/s]、
[m/s]、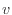 [m/s]、
[m/s]、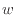 [m/s]、
[m/s]、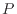 [Pa]、
[Pa]、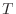 [K]、
[K]、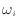 [kg/kg]の6つである。式の数が6つであるので、式を解くことで未知数を求めることができる。
[kg/kg]の6つである。式の数が6つであるので、式を解くことで未知数を求めることができる。
すべての保存式において
の形となっている。時間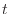 [s]で微分されている非定常項、速度ベクトル
[s]で微分されている非定常項、速度ベクトル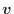 [m/s]との内積をとっている対流項、拡散係数(単位はすべて
[m/s]との内積をとっている対流項、拡散係数(単位はすべて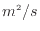 )と
)と
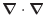 の項で表される拡散項と残りの項である。それぞれ質量(と比熱)あたりの物理量に対応している。運動量保存式では運動量
の項で表される拡散項と残りの項である。それぞれ質量(と比熱)あたりの物理量に対応している。運動量保存式では運動量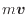 が質量あたりであるので
が質量あたりであるので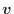 となる。エネルギー保存では非圧縮では内部エネルギー
となる。エネルギー保存では非圧縮では内部エネルギー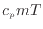 のみとなり比熱
のみとなり比熱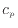 と質量あたりは
と質量あたりは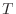 となる。成分の質量
となる。成分の質量
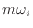 の質量あたりは
の質量あたりは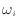 となる。また、質量保存では、質量
となる。また、質量保存では、質量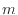 の質量あたりであるので
の質量あたりであるので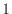 であり、二階微分の項はゼロとなり消える。
であり、二階微分の項はゼロとなり消える。



Next: A. 付録
Up: 2.6 一般形
Previous: 2.6.0.1 圧縮性流体(密度 [kg/m ]は変化する)
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
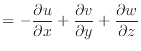

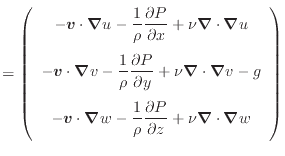
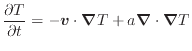
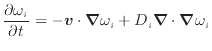
![]() [kg/m
[kg/m![]() ]、
]、![]() [m
[m![]() /s]、
/s]、![]() [m/s
[m/s![]() ]、
]、![]() [J/(kg
[J/(kg![]() K)]、
K)]、![]() [W/(K
[W/(K![]() m)]、
m)]、![]() [m
[m![]() /s])を除くと未知数は
/s])を除くと未知数は![]() [m/s]、
[m/s]、![]() [m/s]、
[m/s]、![]() [m/s]、
[m/s]、![]() [Pa]、
[Pa]、![]() [K]、
[K]、![]() [kg/kg]の6つである。式の数が6つであるので、式を解くことで未知数を求めることができる。
[kg/kg]の6つである。式の数が6つであるので、式を解くことで未知数を求めることができる。