• 学問 -top-

2.3.2 対数-対数　両対数グラフ

対数-対数グラフで直線で表された次のべき関数の式を基本とする。

$$y = 0.8 x ^2$$ (3)

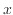$x$ 方向に10ずらした式(10)、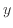$y$ 方向に20ずらした式(11)、定数をそれぞれ変えた式(12)と式(13)がどう変わるか見ていく。

$$y = 0.8 (x - 10)^2$$ (10)

$$y = 0.8 x^2 + 2000$$ (11)

$$y = 1.3 x^2$$ (12)

$$y = 0.8 x^3$$ (13)

式(10)を変形する。 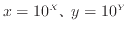$x = 10 ^X、 y = 10 ^Y$ を代入し、両辺の10の対数を取る。

$$y = 0.8 (x - 10)^2$$

$$10 ^Y = 0.8 (10^X - 10)^2$$

$$\log_{10} 10 ^Y = \log_{10} \{0.8 (10^X - 10)^2\}$$

$$Y = 2 \log_{10} (10^X -10) + \log_{10} 0.8$$

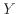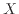$Y$ と$X$ は線形関数にはならず、図12(b)でも直線ではなく上に凸な曲線になっている。しかし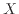$X$ が大きくなるにつれて式3の直線に近づいていく。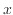$x$ 方向にゼロ点がずれると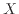$X$ が小さな領域では直線とならず、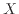$X$ が大きくなるにつれて直線に近づくことが分かる。

式(11)を変形する。 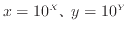$x = 10 ^X、 y = 10 ^Y$ を代入し、両辺の10の対数を取る。

$$y = 0.8 x^2 + 2000$$

$$10 ^Y = 0.8 (10^X)^2 +2000$$

$$\log_{10} 10 ^Y = \log_{10} \{ 0.8 (10^X)^2 +2000 \}$$

$$Y = \log_{10} \{ 0.8 (10^X)^2 +2000 \}$$

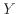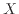$Y$ と$X$ は線形関数にはならず、図12(b)でも直線ではなく下に凸な曲線になっている。しかし式(10)と同様に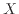$X$ が大きくなるにつれて式3の直線に近づいていく。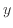$y$ 方向にゼロ点がずれた場合でも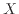$X$ が小さな領域では直線とならず、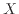$X$ が大きくなるにつれて直線に近づく。

式(12)を変形する。 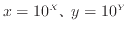$x = 10 ^X、 y = 10 ^Y$ を代入し、両辺の10の対数を取る。

$$y = 1.3 x^2$$

$$10 ^Y = 1.3 (10^X)^2$$

$$\log_{10} 10 ^Y = \log_{10} \{ 1.3 (10^X)^2 \}$$

$$Y = 2 X + \log_{10} 1.3$$

$$Y \simeq 2 X + 0.1139$$

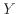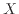$Y$ と$X$ は線形の関係となり、図12(b)でも直線となる。表1に示すように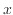$x$ の係数が変わると両対数グラフ（図12(b)）での切片が変わる。

式(13)を変形する。 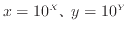$x = 10 ^X、 y = 10 ^Y$ を代入し、両辺の10の対数を取る。

$$y = 0.8 x^3$$

$$10 ^Y = 0.8 (10^X)^3$$

$$\log_{10} 10 ^Y = \log_{10} \{ 0.8 (10^X)^3 \}$$

$$Y = 3 X + \log_{10} 0.8$$

$$Y \simeq 3 X - 0.09691$$

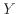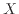$Y$ と$X$ は線形の関係となり、図12(b)でも直線となる。表1に示すように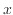$x$ の指数が変わると両対数グラフ（図12(b)）での傾きが変わる。

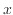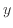べき関数は両対数グラフで、定数が変わっても直線で表されるが、$x$ 方向や$y$ 方向にずれた場合には値の小さな領域で直線から外れる。

図 12: 対数-対数グラフでの比較

(a) 線形グラフ

(b) 両対数グラフ

関連する記事

・この記事の新しい版
対数グラフ 2020.03.25版

• 学問 -top-

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。