

Next: 2.3 詳細な性質
Up: 2 なぜ対数グラフを使うのか
Previous: 2.1.4 対数-対数 両対数グラフ
どの関数がどのグラフで直線で描かれたか表1に纏める。
関係のわからないあるデータが得られた時に、普通のグラフに描き直線状に分布すれば線形関数(
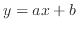 )であることが分かる。曲線の場合には図7に示すようにグラフからどのような関数であるか判別することは難しい。しかし、対数グラフにおいて直線状に分布すればどのような関係にあるか分かる。図8の片対数グラフで直線の関係が得られれば指数関数(
)であることが分かる。曲線の場合には図7に示すようにグラフからどのような関数であるか判別することは難しい。しかし、対数グラフにおいて直線状に分布すればどのような関係にあるか分かる。図8の片対数グラフで直線の関係が得られれば指数関数(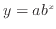 )、図9の片対数グラフで直線の関係が得られれば対数関数(
)、図9の片対数グラフで直線の関係が得られれば対数関数(
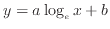 )、図10の両対数グラフで直線の関係が得られればべき関数(
)、図10の両対数グラフで直線の関係が得られればべき関数(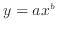 )である。また、そのグラフの傾きと切片を読みとれば、具体的な関数の形を求められる。直線となる関数と対数グラフでの傾きと切片を纏めて表1に示している。例えば図10の両対数グラフの赤線で表されているべき関数の直線を見てみる。緑で描かれた
)である。また、そのグラフの傾きと切片を読みとれば、具体的な関数の形を求められる。直線となる関数と対数グラフでの傾きと切片を纏めて表1に示している。例えば図10の両対数グラフの赤線で表されているべき関数の直線を見てみる。緑で描かれた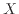 軸と
軸と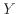 軸で傾きを読みとると、横軸の
軸で傾きを読みとると、横軸の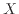 が1増えると縦軸の
が1増えると縦軸の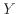 は2増えているので傾きは2、横軸
は2増えているので傾きは2、横軸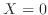 で縦軸
で縦軸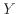 は -0.1程度であるので切片は約-0.1である。表1の両対数グラフの行から
は -0.1程度であるので切片は約-0.1である。表1の両対数グラフの行から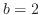 、
、
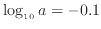 であり
であり
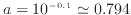 とほぼ元の関数の
とほぼ元の関数の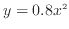 を読みとることが出来る。このように詳細の分からない関数でも、対数グラフに描くことで式の形が分かることがある。
を読みとることが出来る。このように詳細の分からない関数でも、対数グラフに描くことで式の形が分かることがある。
表 1:
各グラフで直線となる関数
| グラフ |
直線になる関数 |
式 |
グラフ上での傾き |
グラフ上での切片 |
| 線形グラフ(線形-線形) |
線形関数 |
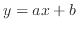
|
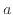
|
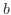
|
| 片対数グラフ(線形-対数) |
指数関数 |
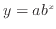
|

|

|
| 片対数グラフ(対数-線形) |
対数関数 |
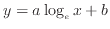
|
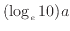
|
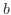
|
| 両対数グラフ(対数-対数) |
べき関数 |
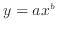
|
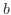
|

|


Next: 2.3 詳細な性質
Up: 2 なぜ対数グラフを使うのか
Previous: 2.1.4 対数-対数 両対数グラフ
関連する記事
・この記事の新しい版
対数グラフ 2020.03.25版
この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。