• 学問 -top-

2.1.3 対数-線形　片対数グラフ

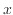$x$ 軸が対数となる片対数グラフでは図9のようになる。

図 9: 片対数グラフ

線形関数の式(2)を変形する。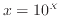$x = 10 ^X$ を代入し変形する。

$$y = 90 x + 500$$

$$y = 90 \times 10 ^X + 500$$

$$y \simeq 10^{X + 1.954} + 500$$

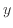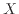$y$ と$X$ は指数関数に近い形となり、図9の線形関数を表す黒線は線形-線形グラフ（図7）の指数関数（青線）と近い下に凸の曲線になっている。

べき関数の式(3)を変形する。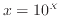$x = 10 ^X$ を代入し変形する。

$$y = 0.8 x ^2$$

$$y = 0.8 (10 ^X ) ^2$$

$$y = 0.8 (10^2)^X$$

$$y = 0.8 \times 100^X$$

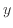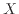$y$ と$X$ は指数関数となり、図9のべき関数を表す赤線は線形-線形グラフ（図7）の指数関数（青線）と近い下に凸の曲線になっている。

指数関数の式(4)を変形する。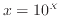$x = 10 ^X$ を代入し変形する。

$$y = 0.9 \times 1.1^x$$

$$y = 0.9 \times 1.1^{10 ^X}$$

$$y = 0.9 \times (1.1^{10})^X$$

$$y \simeq 0.9 \times 2.594 ^X$$

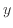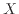$y$ と$X$ は指数関数となり、図9の指数関数を表す青線は線形-線形グラフ（図7）の指数関数（青線）と近い下に凸の曲線になっている。

対数関数の式(5)を変形する。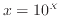$x = 10 ^X$ を代入し変形する。

$$y = 2000 \log_{e}x +1000$$

$$y = 2000 \log_{e} 10 ^X + 1000$$

$$y = 2000 X \log_{e} 10 + 1000$$

$$y \simeq 2000 \times 2.303 X + 1000$$

$$y \simeq 4606 X + 1000$$

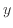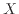$y$ と$X$ は線形関数となり、図9では対数関数を表す緑線は直線として描かれる。定数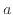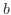$a$ 、$b$ で表される対数関数を同様に変形する。

$$y = a\log_e x + b$$

$$y = a \log_e 10^X + b$$

$$y = (\log_e 10) a X + b$$

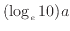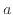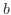このようにグラフの傾きが $(\log_e 10) a$ 、切片がbとなる。グラフから読みとった傾きと切片から元の関数の$a$ と$b$ を求めることができる。

関連する記事

・この記事の新しい版
対数グラフ 2020.03.25版

• 学問 -top-

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 国際 ライセンスの下に公開する。最新版はhttp://camellia.thyme.jpで公開している。