B 熱力学第二法則とエントロピーの付録 B.7 サイクルの比較 C 熱力学第零法則と温度の付録

B.8 可逆変化の熱

可逆変化の熱によりエントロピーを定義した。ではエントロピー変化を現実の不可逆変化で求めるためには、この可逆変化での熱はどのように考えればよいのだろうか。

B.8.1 不可逆変化を可逆変化で表す

不可逆変化を可逆変化で表すことで可逆の熱を考えることができる。まず可逆変化について確認をする。可逆変化となる過程は可逆断熱過程と準静等温過程のみである（詳しくは5.4.2節 ${}^{\text{p.\ref{sec-ReversibleCycleProcess}}}$ ）。可逆断熱過程は発熱もなく熱が伝わることもない過程であり、準静等温過程は系と熱源の温度を限りなく近づけ無限の時間をかけて熱を伝える過程である。可逆断熱過程では熱のやりとりはないので、可逆過程での熱のやりとりは必ず準静等温過程で行われる。

不可逆で熱を受け取った場合の系のエントロピーの変化をどう扱えばよいか考えていこう。系は十分に小さく温度は一様分布であると扱えるとする。エントロピーの変化量を計算する際に、エントロピーは状態量であるので、始めと終わりの状態が同じであれば、その間の変化がどのような経路でも変化量は同じである。そこで、不可逆変化のエントロピーの変化量を計算するために、同じ始めと終わりの状態から間の変化を可逆断熱過程と準静等温過程のみで構成される経路で考えば、どのような不可逆の変化であってもエントロピーを計算できる。

どんな過程も可逆断熱過程と準静等温過程で表すことが出来る。例えば、まず過程の終わりの温度となるまで可逆断熱過程で変化をさせる。温度は同じになっているので圧力が同じになるまで系を準静等温過程で加熱（冷却）すれば終わりの状態に出来る。この経路の準静等温過程の部分でやり取りされる熱を、不可逆過程においてエントロピー変化を計算する際の可逆過程での熱として計算することが出来る。

準静等温過程を先にする経路と後にする経路では熱量が異なるが、温度も異なるためエントロピーの変化量は等しくなる。状態Aから状態Bへ不可逆で変化する過程を図B.12に示すように可逆過程での変化で表す。状態Aから状態Bへ可逆過程で変化する経路として、先に準静等温過程（熱 $Q_{\mathrm{AC}}$ が伝わる）で状態Cまで変化し後に可逆断熱過程で状態Bへ至る経路１と、先に可逆断熱過程で状態Dまで変化し後に準静等温過程（熱 $Q_{\mathrm{BD}}$ が伝わる）で状態Bへ至る経路２の二つの経路が考えられる。このそれぞれの経路において必ずしも伝わる熱は等しくならない（ $Q_{\mathrm{AC}}\neq Q_{\mathrm{BD}}$ ）。この二つの経路を組み合わせて、A→C→B→D→A⁶⁶6可逆であるためA→D→B→C→Aでもよい。となるサイクルとすると、初めに考えていた不可逆過程の始点と終点を含む可逆サイクル（カルノーサイクル）となる。

Figure B.12: 可逆過程による経路の

P V

線図

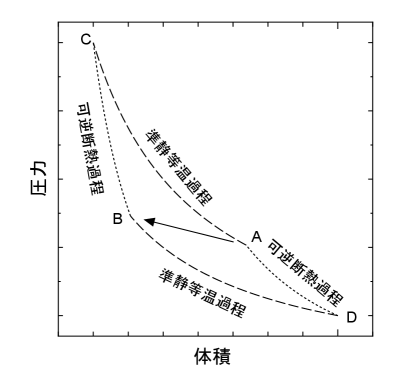
可逆サイクルからどちらの経路でもエントロピーの変化量は等しいことを確認しよう。可逆サイクルでは次式が成り立つ。

\displaystyle\frac{Q_{\mathrm{AC}}}{\varTheta_{\mathrm{A}}}=\frac{Q_{\mathrm{% BD}}}{\varTheta_{\mathrm{B}}}

$\varTheta_{\mathrm{A}}$ は状態Aの温度、 $\varTheta_{\mathrm{B}}$ は状態Bの温度である。また、経路１と経路２のエントロピーの変化量はそれぞれ次の様に表される。

	$\displaystyle\Delta S_{1}$	$\displaystyle=\frac{Q_{\mathrm{AC}}}{\varTheta_{\mathrm{A}}}$
	$\displaystyle\Delta S_{2}$	$\displaystyle=\frac{Q_{\mathrm{BD}}}{\varTheta_{\mathrm{B}}}$

上３式から経路１と経路２でのエントロピーの変化量が等しいことが分かる。

このように、不可逆過程でも可逆断熱過程と準静等温過程に分けることでエントロピー変化量を求めることができる。

B.8.2 具体的な数値による計算

具体的な数値による計算を、窒素（1 cm²）を加熱する場合についてしてみよう。 1 cm³の窒素では局所熱力学的平衡（3.1.2 ${}^{\text{p.\ref{sec-LocalThermodynamicEquilibrium}}}$ ）が成り立っており、一様な温度であるとする。状態量、物性値はCoolProp[5]で計算した。大気圧下で0.01 J加熱したとする。大気圧下で加熱されると等圧で膨張する。

加熱前の窒素の状態は大気圧0.1 MPa、温度20 ℃とする。密度は 1.1888 kg/m³であるので、体積1 cm³の質量は1.14959 mgである。ここから加熱後の状態を計算しよう。加熱後も大気圧下であるので圧力は0.1 MPaである。加熱量の0.01 Jを窒素の等圧比熱1041.3159 J/(kg K)と質量で割ることで温度の変化量8.35 ℃が計算でき、加熱後の温度は28.35 ℃と分かる。 $P-V$ 線図を図B.14に、 $T-S$ 線図を図B.14に示す。それぞれの図中の黒線が加熱による大気圧下での等圧の変化を示している。

Figure B.13: 不可逆と可逆の熱の

P-V

線図

Figure B.14: 不可逆と可逆の熱の

T-S

線図

次に可逆の変化を計算しよう。まず先に断熱変化をする場合は、可逆断熱で加熱後の温度まで変化させる（図B.14、図B.14でのオレンジ点線）。可逆断熱変化はエントロピーが一定で変化しない。加熱前の圧力0.1 MPa、温度20 ℃においてエントロピーが784.21 $\times 10^{-5}$ J/K（比エントロピーが3867.2594 J/(kg K)）である。このエントロピー784.21 $\times 10^{-5}$ J/Kで加熱後の28.36 ℃となる点が可逆断熱変化の終了の状態で、圧力は0.110333 MPaである。次に準静等温変化で温度は28.36 ℃で一定のまま、圧力をさげ0.1 MPaになるまで変化させる。この過程は加熱過程であり、体積とエントロピーは増加する（図B.14、図B.14でのオレンジ破線）。この可逆の過程で作用する熱は0.0101372 Jである。別の過程として、先に準静等温変化で変化後の比エントロピーになるまで変化させ、その後に可逆断熱変化をしてもよい（図B.14、図B.14での青破線→青点線）。この可逆の過程で作用する熱は0.0098561 Jである。

可逆過程の組み合わせは無数にあり、図B.14と図B.14に示したような一組の可逆断熱過程と等温準静過程だけでなく、複数組に分けても良い。二組の可逆断熱過程と等温準静過程での変化を表した $P-V$ 線図を図B.16に、 $T-S$ 線図を図B.16に示す。また、十組の可逆断熱過程と等温準静過程での変化を表した $P-V$ 線図を図B.18に、 $T-S$ 線図を図B.18に示す。図B.18、図B.18に示すように、細かく多くの組に分けることで不可逆の線に近づいていく。どんどん細かく分けていき、無限個に分けると不可逆の線を表すことができる。