B 熱力学第二法則とエントロピーの付録 B.6 準静等温過程での仕事 B.8 可逆変化の熱

B.7 サイクルの比較

サイクルの比較を本文中とは異なる方法でしている説明や、本文中では詳細をあげなかった説明を載せている。

B.7.1 可逆サイクルの効率は等しい（クラウジウスの表現）

可逆サイクルの効率は等しい（クラウジウスの表現）ことを示す。 2.4.3節 ${}^{\text{p.\ref{sec-ReversibleCycleEfficiency}}}$ では可逆サイクルの効率は等しいことを熱力学第二法則トムソンの表現を用いて示した。ここでは同様に可逆サイクルの効率は等しいことを熱力学第二法則クラウジウスの表現を用いて示す。概要を図B.6に示す。

Figure B.6: 可逆サイクルの比較

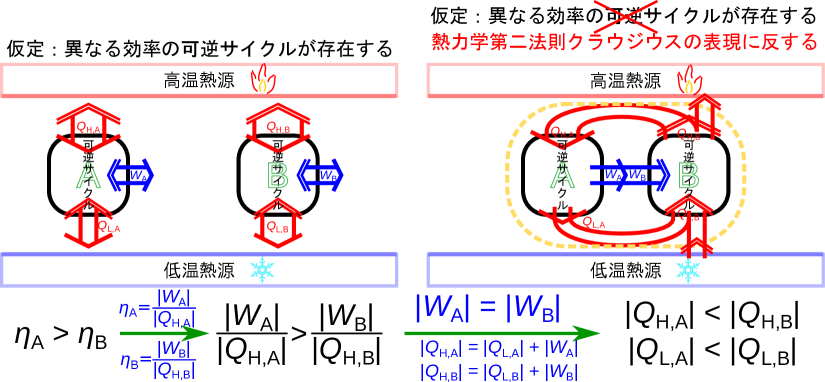
可逆サイクルAと可逆サイクルBを並べて同じ二つの熱源間で動作させる（図B.6-左）。次式のように可逆サイクルAの熱機関としての効率 $\eta_{\mathrm{A}}$ [-]が、可逆サイクルBの熱機関としての効率 $\eta_{\mathrm{B}}$ [-]よりも高いと仮定する。

\displaystyle\eta_{\mathrm{A}}>\eta_{\mathrm{B}}

(B.6)

効率の高い可逆サイクルAを熱機関として、可逆サイクルBをヒートポンプとして、仕事の大きさが同じになるよう（ $|W_{\mathrm{A}}|=|W_{\mathrm{B}}|$ ）に動作させ⁵⁵5それぞれの可逆サイクルの仕事の大きさが違う場合は、同じ可逆サイクルを複数個まとめて動作させて、それぞれの数を調整し、総計で同じ仕事となるように調整する。る（図B.6-右）。熱機関の効率の式(1.20) ${}^{\text{p.\ref{eq-EfficiencyEngine}}}$ と効率の関係の式(B.6) ${}^{\text{p.\ref{eq-InequalityRevCycleEfficiency}}}$ から

\frac{|W_{\mathrm{A}}|}{|Q_{\mathrm{H,A}}|}>\frac{|W_{\mathrm{B}}|}{|Q_{% \mathrm{H,B}}|}

ここで仕事が同じとなるように動作させている（ $|W_{\mathrm{A}}|=|W_{\mathrm{B}}|$ ）ので、次式が成り立つ。

\displaystyle|Q_{\mathrm{H,A}}|<|Q_{\mathrm{H,B}}|

(B.7)

上式と熱機関におけるエネルギー保存の式(1.22) ${}^{\text{p.\ref{eq-CycleEnergyConservation}}}$ とヒートポンプにおけるエネルギー保存の式(1.26) ${}^{\text{p.\ref{eq-CycleEnergyConservationPump}}}$ より、

|Q_{\mathrm{L,A}}|+|W_{\mathrm{A}}|>|Q_{\mathrm{L,B}}|-|W_{\mathrm{B}}|

仕事の大きさが同じになるように動作させている( $|W_{\mathrm{A}}|=|W_{\mathrm{B}}|$ )ので、次の関係が成り立つ。

\displaystyle|Q_{\mathrm{L,A}}|

\displaystyle<|Q_{\mathrm{L,B}}|

(B.8)

図B.6の右側の図のオレンジの点線のように二つのサイクルを大きな一つの系として考えると、高温熱源への熱は式(B.7)より系から高温熱源へ向かっている（図B.6右の右側でオレンジの点線から高温熱源に向かっている赤の矢印）。また、低温熱源からの熱は式(B.8)より系が受け取っている（図2.11右の下側でオレンジの点線へ入っている赤の矢印）。二つのサイクルを含めた大きな系で見ると、系が低温熱源から他に作用を及ぼさず高温熱源に熱が伝わっているため、熱力学第二法則のクラウジウスの表現（2.2節 ${}^{\text{p.\ref{sec-2ndLawStatements}}}$ ）に反する。よって、ある可逆サイクルの効率が他の可逆サイクルの効率よりも高くなることはありえない。

B.7.2 可逆サイクルと不可逆の熱機関の比較

可逆サイクルと不可逆の熱機関の比較をする。可逆サイクルの熱機関としての効率は実在の不可逆の熱機関よりも必ず高くなることを熱力学第二法則から示す。

可逆サイクルと不可逆熱機関の比較（トムソンの表現）

可逆サイクルと不可逆熱機関の比較（トムソンの表現）をする。不可逆の熱機関Eと可逆サイクルRを考える。ここで、不可逆の熱機関Eの効率 $\eta_{\mathrm{E不}}$ が可逆サイクルRの効率 $\eta_{\mathrm{R可}}$ よりも高いと仮定しよう（図B.7-左）。この仮定をした結果、熱力学第二法則（トムソンの表現）に反することで、この仮定が間違っていることを示す。

Figure B.7: 可逆サイクルと不可逆熱機関の比較

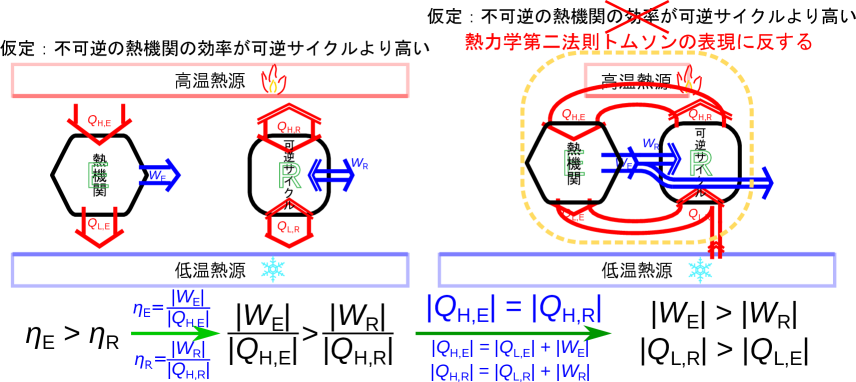
不可逆の熱機関の効率が可逆サイクルの効率より高い仮定から次式が示される。

\displaystyle\eta_{\mathrm{E不}}

\displaystyle>\eta_{\mathrm{R可}}

効率の関係の式(1.20) ${}^{\text{p.\ref{eq-EfficiencyEngine}}}$ から、次式が成り立つ。

\displaystyle\frac{|W_{\mathrm{E}}|}{|Q_{\mathrm{H,E}}|}

\displaystyle>\frac{|W_{\mathrm{R}}|}{|Q_{\mathrm{H,R}}|}

可逆サイクルRはヒートポンプとしても動作できる（図B.7-右）ので、不可逆の熱機関Eが高温熱源に受け渡す熱と同じだけの熱を受け取る（ $|Q_{\mathrm{H,E}}|=|Q_{\mathrm{H,R}}|$ ）可逆ヒートポンプとして動作させる（図B.7-右）と次式が成り立つ。

\displaystyle|W_{\mathrm{E}}|>|W_{\mathrm{R}}|

(B.9)

エネルギーの保存式(1.22)と式(1.26)と、高温熱源側の熱の大きさの関係（ $|Q_{\mathrm{H,E}}|=|Q_{\mathrm{H,R}}|$ ）から、

\displaystyle|Q_{\mathrm{L,R}}|>|Q_{\mathrm{L,E}}|

(B.10)

図B.7の右側の図のオレンジの点線のように高温熱源も含めた大きな一つの系として考えると、全体での仕事は式(B.9)より系から取り出されている。また、低温熱源からの熱は式(B.10)より系が受け取っている。大きな系で見ると、系が低温熱源（一つの熱源）から熱を受け取り仕事に変換しているため、熱力学第二法則のトムソンの表現（2.2節 ${}^{\text{p.\ref{sec-2ndLawStatements}}}$ ）に反する。よって、実在する不可逆の熱機関の効率が可逆サイクルの効率よりも高くなることはありえない。可逆サイクルの熱機関としての効率は、同じ二つの熱源を用いる中では最も高い。また、二つの熱源が決まれば可逆サイクルの効率も決まる。

可逆サイクルと不可逆熱機関の比較（クラウジウスの表現）

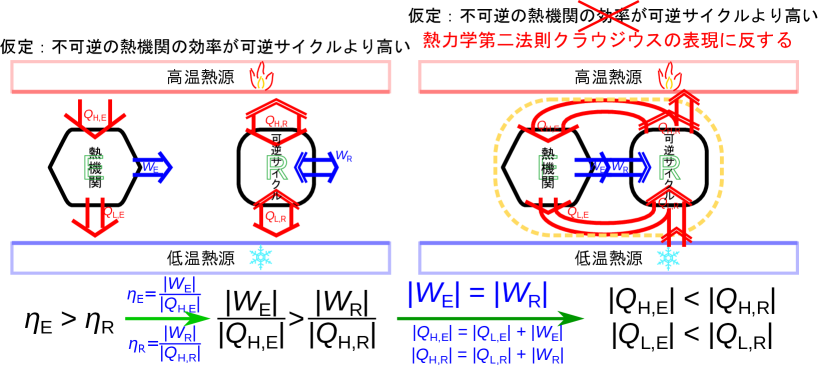
可逆サイクルと不可逆熱機関の比較（クラウジウスの表現）をする。先ほどと同じように不可逆の熱機関Eと可逆サイクルRを考える。ここで、不可逆の熱機関Eの効率 $\eta_{\mathrm{E不}}$ が可逆サイクルRの効率 $\eta_{\mathrm{R可}}$ よりも高いと仮定しよう（図B.8-左）。この仮定をした結果、熱力学第二法則（クラウジウスの表現）に反することで、この仮定が間違っていることを示す。

\displaystyle\eta_{\mathrm{E不}}

\displaystyle>\eta_{\mathrm{R可}}

効率の関係の式(1.20) ${}^{\text{p.\ref{eq-EfficiencyEngine}}}$ から、次式が成り立つ。

\displaystyle\frac{|W_{\mathrm{E}}|}{|Q_{\mathrm{H,E}}|}

\displaystyle>\frac{|W_{\mathrm{R}}|}{|Q_{\mathrm{H,R}}|}

可逆熱機関Bは可逆でありヒートポンプとしても動作できるので、不可逆熱機関Aが周囲に受け渡す仕事と同じだけ仕事を受け取る（ $|W_{\mathrm{E}}|=|W_{\mathrm{R}}|$ ）可逆ヒートポンプとして動作させる（図B.8-右）と次式が成り立つ。

\displaystyle|Q_{\mathrm{H,E}}|

\displaystyle<|Q_{\mathrm{H,R}}|

熱機関とヒートポンプのエネルギーの保存式(1.22)と式(1.26)と、仕事の大きさの関係（ $|W_{\mathrm{E}}|=|W_{\mathrm{R}}|$ ）から、

|Q_{\mathrm{L,E}}|<|Q_{L,R}|

となり、図B.8-右のように周囲になにも変化を残さず、低温熱源から( $|Q_{\mathrm{L,R}}|-|Q_{\mathrm{L,E}}|$ )[J]または( $|Q_{\mathrm{H,R}}|-|Q_{\mathrm{H,R}}|$ )[J]を高温熱源へ伝えることが出来てしまう。よって可逆熱機関よりも効率の良い不可逆熱機関は熱力学第二法則クラウジウスの表現（2節 ${}^{\text{p.\ref{sec-2ndLaw}}}$ ）に反する。このことから可逆熱機関の効率が必ず高くなるといえる。

Figure B.8: 可逆熱機関と不可逆熱機関の比較

不可逆熱機関Eの効率 $\eta_{\mathrm{E不}}$ が可逆熱機関Rの効率 $\eta_{\mathrm{R可}}$ よりも低い場合には熱力学第二法則に反することはないことを次節で示す。

B.7.3 可逆サイクルの効率が不可逆熱機関より高い場合

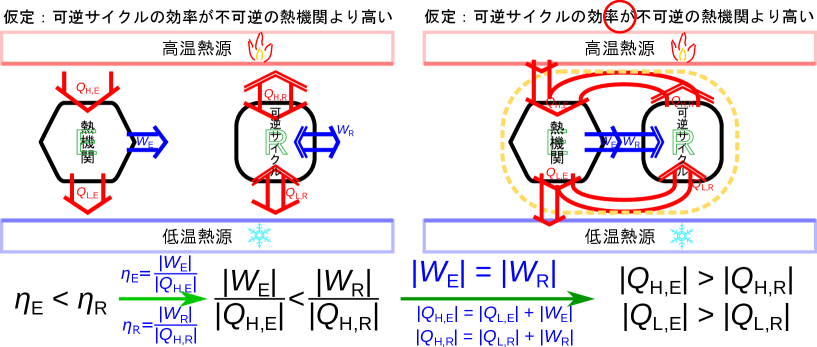
可逆サイクルの効率が不可逆熱機関より高い場合には熱力学第二法則に合う現象である。可逆熱機関の効率が不可逆熱機関の効率よりも低いと熱力学第二法則に反することを前節（B.7.2節 ${}^{\text{p.\ref{sec-ReversibleIrreversibleCycleEfficiency}}}$ ）に示した。ここでは不可逆の熱機関Eの効率 $\eta_{\mathrm{E,不}}$ [-]が可逆熱機関Rの効率 $\eta_{\mathrm{R,可}}$ [-]よりも低い場合には熱力学第二法則に反しないことを示す（図B.9）。

\displaystyle\eta_{\mathrm{E不}}

\displaystyle<\eta_{\mathrm{R可}}

式(1.25) ${}^{\text{p.\ref{eq-EfficiencyPump}}}$ より次式が成り立つ。

\displaystyle\frac{|W_{\mathrm{E}}|}{|Q_{\mathrm{E,H}}|}

\displaystyle<\frac{|W_{\mathrm{R}}|}{|Q_{\mathrm{R,H}}|}

不可逆の熱機関Eは逆にヒートポンプとして動作させることはできない。可逆サイクルRはヒートポンプとしても動作できるので、不可逆の熱機関Aと同じ大きさの仕事で（ $|W_{\mathrm{E}}|=|W_{\mathrm{R}}|$ ）ヒートポンプとして動作させる（図B.9-右）と次式が成り立つ。

\displaystyle|Q_{\mathrm{H,E}}|>|Q_{\mathrm{H,R}}|

全体として高温熱源から低温熱源に熱が伝わっている（図B.9-右）ので、熱力学第二法則に反しない。

Figure B.9: 可逆サイクルと不可逆サイクルの比較

B.7.4 可逆サイクルと不可逆のヒートポンプの比較

可逆サイクルと不可逆のヒートポンプの比較をする。可逆サイクルのヒートポンプしての成績係数は実在のヒートポンプよりも必ず高くなることを熱力学第二法則から示す。

可逆サイクルと不可逆ヒートポンプの比較（トムソンの表現）

可逆サイクルと不可逆ヒートポンプの比較（トムソンの表現）をする。ここで、不可逆ヒートポンプPの成績係数が可逆サイクルRのヒートポンプとしての成績係数よりも高いと仮定し、熱力学第二法則トムソンの表現に反することから可逆サイクルの成績係数が現実の不可逆ヒートポンプよりも高くなることを示す（図B.10）。

成績係数の関係の仮定から次式が成り立つ。

\displaystyle\epsilon_{\mathrm{R可}}

\displaystyle<\epsilon_{\mathrm{P}}

上式と成績係数の式(1.25) ${}^{\text{p.\ref{eq-EfficiencyPump}}}$ より次式が成り立つ。

\displaystyle\frac{|Q_{\mathrm{H,R}}|}{|W_{\mathrm{R}}|}

\displaystyle<\frac{|Q_{\mathrm{H,P}}|}{|W_{\mathrm{P}}|}

可逆サイクルRは熱機関としても動作できるので、高温熱源とやりとりする熱の絶対値の大きさを不可逆ヒートポンプPと同じ大きさ（ $|Q_{\mathrm{H,R}}|=|Q_{\mathrm{H,P}}|$ ）とし熱機関として動作させる（図B.10-右）と次式が成り立つ。

\displaystyle|W_{\mathrm{R}}|

\displaystyle>|W_{\mathrm{P}}|

熱機関とヒートポンプのエネルギーの保存式(1.22)と式(1.26)と、仕事の大きさの関係（ $|Q_{\mathrm{H,R}}|=|Q_{\mathrm{H,P}}|$ ）から、

\displaystyle|Q_{\mathrm{L,R}}|

\displaystyle>|Q_{\mathrm{L,P}}|

の関係が成り立つ。このことから、一つの熱源（低温熱源）から $|Q_{\mathrm{L,P}}|-|Q_{\mathrm{L,R}}|$ を受け取り仕事 $|W_{\mathrm{R}}|-|W_{\mathrm{P}}|$ を取り出すことが出来てしまう（図B.10-右）。よって可逆ヒートポンプよりも効率の良い不可逆ヒートポンプは熱力学第二法則トムソンの表現に反する。よって仮定した不可逆ヒートポンプの成績係数が可逆サイクルのヒートポンプとしての成績係数よりも高いことは間違いであることが分かる。つまり、可逆サイクルのヒートポンプとしての成績係数は現実の不可逆ヒートポンプの成績係数よりも高いことが示された。

Figure B.10: 可逆サイクルと不可逆ヒートポンプの比較（トムソンの表現）

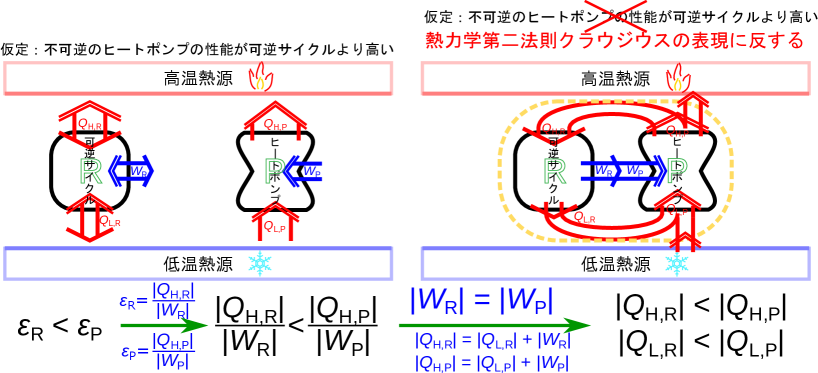
可逆サイクルと不可逆ヒートポンプの比較（クラウジウスの表現）

可逆サイクルと不可逆ヒートポンプの比較（クラウジウスの表現）をする。ここでは、不可逆ヒートポンプPの成績係数が可逆サイクルRのヒートポンプとしての成績係数よりも高いと仮定し、熱力学第二法則クラウジウスの表現に反することから可逆サイクルの成績係数が現実の不可逆ヒートポンプよりも高くなることを示す（図B.11）。成績係数の関係の仮定から次式が成り立つ。

\displaystyle\epsilon_{\mathrm{R可}}

\displaystyle<\epsilon_{\mathrm{P}}

上式と成績係数の式(1.25) ${}^{\text{p.\ref{eq-EfficiencyPump}}}$ より次式が成り立つ。

\displaystyle\frac{|Q_{\mathrm{H,R}}|}{|W_{\mathrm{R}}|}

\displaystyle<\frac{|Q_{\mathrm{H,P}}|}{|W_{\mathrm{P}}|}

可逆サイクルRは熱機関としても動作できるので、不可逆ヒートポンプPと同じ大きさの仕事で（ $|W_{\mathrm{R}}|=|W_{\mathrm{P}}|$ ）熱機関として動作させる（図B.11-右）と次式が成り立つ。

\displaystyle|Q_{\mathrm{H,R}}|

\displaystyle<|Q_{\mathrm{H,P}}|

熱機関とヒートポンプのエネルギーの保存式(1.22)と式(1.26)と、仕事の大きさの関係（ $|W_{\mathrm{R}}|=|W_{\mathrm{P}}|$ ）から、

\displaystyle|Q_{\mathrm{L,R}}|

\displaystyle<|Q_{\mathrm{L,P}}|

の関係が成り立つ。このことから、周囲になにも変化を残さず、低温熱源から $|Q_{\mathrm{H,P}}|-|Q_{\mathrm{H,R}}|$ ( = $|Q_{\mathrm{L,P}}|-|Q_{\mathrm{L,R}}|$ )を高温熱源へ伝えることが出来てしまう（図B.11-右）。よって可逆ヒートポンプよりも効率の良い不可逆ヒートポンプは熱力学第二法則クラウジウスの表現に反する。よって仮定した不可逆ヒートポンプの成績係数が可逆サイクルのヒートポンプとしての成績係数よりも高いことは間違いであることが分かる。つまり、可逆サイクルのヒートポンプとしての成績係数は現実の不可逆ヒートポンプの成績係数よりも高いことが示された。

以上のように、熱機関としてもヒートポンプとしても同じ効率で動作できる可逆サイクル（可逆熱機関・可逆ヒートポンプ）では逆の働きをさせることが出来るため、可逆サイクルの効率・成績係数よりも不可逆熱機関や不可逆ヒートポンプの効率・成績係数が高いと熱力学の第二法則クラウジウスの表現に反する。このことから、同じ二つの熱源間で動作する可逆サイクル（熱機関・可逆ヒートポンプ）の効率は必ず不可逆熱機関や不可逆ヒートポンプの効率よりも高くなる。

\displaystyle\eta_{\mathrm{可}}\geq\eta_{\mathrm{不}}

(B.11)

\epsilon_{\mathrm{可}}\geq\epsilon_{\mathrm{不}}

Figure B.11: 可逆サイクルと不可逆ヒートポンプの比較（クラウジウスの表現）

B.6 準静等温過程での仕事 References B.8 可逆変化の熱

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。