2.4 可逆サイクル（可逆熱機関・可逆ヒートポンプ）の効率と熱力学的温度

可逆サイクル（可逆熱機関・可逆ヒートポンプ）の効率と熱力学的温度の関係を示していく。熱力学第二法則から熱機関の理想的な最大効率を求める。この最大効率の検討のため、可逆熱機関（可逆ヒートポンプ）を仮定して特徴を考える。可逆熱機関（可逆ヒートポンプ）をまとめて可逆サイクルと呼ぶ。可逆サイクルを考えると、熱機関とヒートポンプの効率の限界を求めることや、温度を定義することができる。ここで考える可逆サイクルは理想的な熱機関・ヒートポンプであり現実には存在しない。その熱機関の最大効率と熱力学的温度との関係を明らかにし、エントロピーの定義へと繋げる。

2.4.1 可逆サイクル（可逆熱機関・可逆ヒートポンプ）

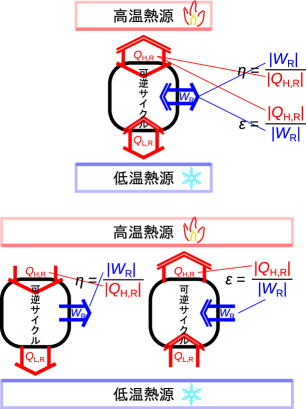
可逆サイクル（可逆熱機関・可逆ヒートポンプ）の特徴をまず示す。図2.7に可逆サイクルと高温熱源、低温熱源との関係を示す。今後は図2.7中の上部のように可逆サイクルを表す。図の下部に示すように一重線の矢印は熱機関として動作した際の熱と仕事の方向を表し、逆向きの二重線の矢印はヒートポンプとして動作する際の熱と仕事が作用すると方向を表している。この熱と仕事の矢印が全く同じ大きさで方向のみを変えられるサイクルは、逆の動きが可能なので、可逆熱機関や可逆ヒートポンプと呼ばれる。ここではまとめて可逆サイクルと呼び、図2.7のように丸みのある四角で表す。可逆サイクルは理論上のサイクルで、実際に作ることはできない。図2.7中にも示した式(1.20)と式(1.25)から可逆サイクルにおいてはヒートポンプの成績係数 $ε$ は熱機関の効率 $η$ の逆数で表され、どちらかが決まればもう一つも決まり、熱機関の効率とヒートポンプの成績係数は反比例の関係にある。

Figure 2.7: 可逆サイクル

2.4.2 実在する熱機関、ヒートポンプと可逆サイクル

実在する熱機関、ヒートポンプと可逆サイクルを比較することで、可逆サイクルが実在するとすればどのようなものになるのか考えてみよう。図2.7に示した可逆サイクルの高温熱源温度が40℃、低温熱源温度が10℃で実際に使われているヒートポンプと熱機関を考えると、冬期につかうヒートポンプ給湯器と海洋温度差発電所が近い温度で使われている。このヒートポンプ給湯器と海洋温度差発電所を例に可逆サイクルが実在するとどのように働くのか見ていく。

ヒートポンプ給湯器は電力を仕事 $W_{\mathrm{R}}$ として供給され低温熱源である周囲の空気から熱 $Q_{\mathrm{L,R}}$ を奪い、仕事と奪った熱の合計分の熱 $Q_{\mathrm{H,R}}$ で高温熱源のお湯を加熱して給湯をする。一般的に売られているヒートポンプ給湯器の成績係数 $ε$ は4程度である。すなわち与えられた仕事（電力）の四倍の加熱ができる。海洋温度差発電所では暖かい海域の表面付近の海水を高温熱源、深さ100 m程度より深い温度の低い海洋深層水を低温熱源として、表層の海水からの熱 $Q_{\mathrm{H,R}}$ から仕事 $W_{\mathrm{R}}$ を取り出し、海洋深層水に $Q_{\mathrm{L,R}}$ を伝える。海洋温度差発電での発電効率 $η$ を0.03程度とすると、表層の海水から受け取った熱の3 %程度を仕事として取り出している。

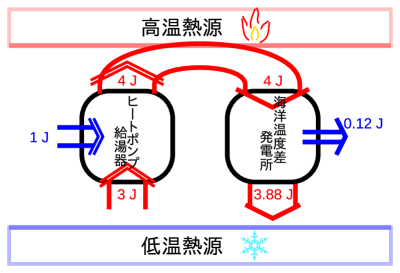
ヒートポンプ給湯器と海洋温度差発電所を並べて、ヒートポンプ給湯器に1 Jの仕事を与えて動かすと、低温熱源から3 J受け取り、高温側の熱源に4 J伝えることができる。この高温熱源で受け取った4 Jを海洋温度差発電所に伝えると、0.12 Jの仕事を周囲にして、残りの3.88 Jは低温熱源へ渡す（図2.8）。その後さらに、この得られた0.12 Jの仕事をヒートポンプ給湯器に与えると、低温熱源から0.36 J受け取り、高温側の熱源に0.48 J伝えることになり、伝える熱の大きさは小さくなる。このようにヒートポンプ給湯器と海洋温度差発電所で仕事のやりとりを続けると、ヒートポンプ給湯器に入れた仕事に対して海洋温度差発電所から受け取る仕事は0.12倍となり、どんどんエネルギー量が減っていき、停止してしまう。

Figure 2.8: ヒートポンプ給湯器と海洋温度差発電所

海洋温度差発電所とヒートポンプ給湯器が、同じ熱と仕事の比で可逆として動作可能だとするとどうなるだろうか。ヒートポンプ給湯器はヒートポンプでは与えた仕事に対して4倍の熱をお湯に与えている。同じ比で熱機関として動作できるとすると、逆-ヒートポンプ給湯器はお湯から受け取った熱の1/4の仕事を取り出すことができる。すなわち効率 $η$ は0.25である。実際に存在する海洋温度差発電所よりかなり大きくなる。海洋温度差発電所は熱機関として高温熱源から受け取った熱から0.03倍の仕事を取り出しているので、同じ量でヒートポンプとして動作できるとすると、逆-海洋温度差発電所は0.03の仕事を受け取って1の熱を高温熱源に伝えることになる。すなわち受け取った仕事の33.3倍程度の熱を高温熱源に伝えることができる。これは実在するヒートポンプ給湯器の成績係数の4よりも大幅に大きくなる。

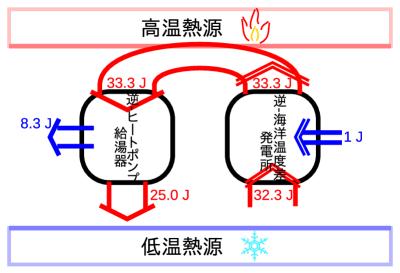
この逆に動作させた逆-ヒートポンプ給湯器と逆-海洋温度差発電所を並べて動作させることを考えてみる。逆-海洋温度差発電所に1 Jの仕事を与えて動かすと、32.3 J程度の熱を低温熱源から受け取り、33.3 J程度の熱を高温熱源に伝えることになる。この高温熱源が受け取った33.3 Jを、そのまま逆-ヒートポンプ給湯器に渡すと、約8.3 Jの仕事を取り出し、25.0 Jの熱を低温熱源に伝える。全体では、はじめに1 Jの仕事与えて、低温熱源から正味7.3 Jの熱を受け取り、8.3 Jの仕事を取り出すことができている。しかも、取り出した8.3 Jを再び逆-海洋温度差発電所に与えて動かすと逆-ヒートポンプ給湯器から約68.9 Jの仕事を取り出すことができ、これを繰り返すごとに得られる仕事は大きくなる（図2.9）。このような装置が実在すればどんどん仕事が得られ発電することができ、夢のような装置であるが、残念ながら逆向きに動作させても同じ熱と仕事の比で動作することはないので、このような逆-ヒートポンプ給湯器と逆-海洋温度差発電所は存在しない。高温熱源と逆-ヒートポンプ給湯器、逆-海洋温度差発電所を一つの系としてとらえれば、この系は一つの熱源（低温熱源）から仕事を取り出しているので、熱力学第二法則のトムソンの表現（2.2節 ${}^{\text{p.\ref{sec-2ndLawStatements}}}$ ）に反することからも、このような装置は存在しないことが分かる。

Figure 2.9: 逆-ヒートポンプ給湯器と逆-海洋温度差発電所

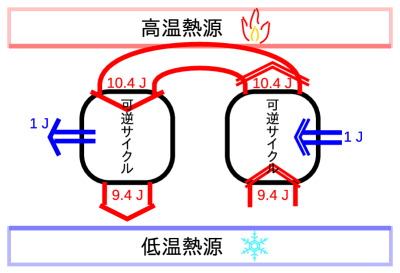
これまで条件として考えてきた高温熱源40 ℃と低温熱源10 ℃の熱源で可逆サイクルを動作させると、後（2.4.6節 ${}^{\text{p.\ref{sec-AbsoluteTemperature}}}$ ）に詳細を記載するように、熱機関の効率は熱源の絶対温度の比((313.15 K - 283.15 K) / 313.15 K)で表され約0.0958であり、その逆数でヒートポンプの成績係数は約10.4となる。可逆サイクルの場合には熱機関とヒートポンプの熱と仕事の比は同じ大きさなので、永久に熱と仕事のやりとりを続けることができる（図2.10）。可逆サイクルは現実には存在しないが、熱力学の考え方を進める上で必要であるので、想像上の理想的なものとして考えていく。

Figure 2.10: 可逆サイクルの組み合わせ

2.4.3 可逆サイクルの効率と熱源

可逆サイクルの効率と熱源の関係として、二つの熱源間で動作する可逆サイクルの熱機関効率はどのような可逆サイクルでも常に等しくなることを、二つの熱源間で動作する可逆サイクル（可逆熱機関・可逆ヒートポンプ）の効率（仕事と熱の比）が異なる場合には熱力学第二法則に反することから示す。

異なる効率の可逆サイクル

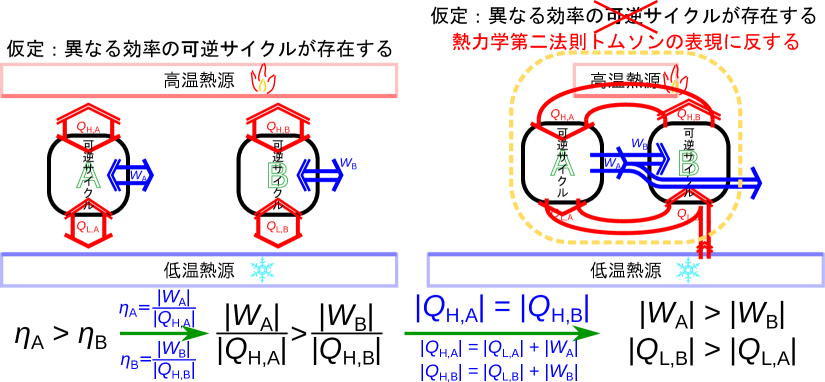
異なる効率の可逆サイクルは同じ二つの熱源では成り立たないことから示す。可逆サイクルAと可逆サイクルBを並べて同じ二つの熱源間で動作させる（図2.11-左）。次式のように可逆サイクルAの熱機関としての効率 $\eta_{\mathrm{A}}$ [-]が、可逆サイクルBの熱機関としての効率 $\eta_{\mathrm{B}}$ [-]よりも高いと仮定する。

Figure 2.11: 可逆サイクルの比較

\displaystyle\eta_{\mathrm{A}}>\eta_{\mathrm{B}}

(2.1)

効率の高い可逆サイクルAを熱機関として、可逆サイクルBをヒートポンプとして、高温熱源とやりとりする熱の大きさが同じになるよう（ $|Q_{\mathrm{H,A}}|=|Q_{\mathrm{H,B}}|$ ）に動作させる⁶⁶6それぞれの可逆サイクルの熱の大きさが違う場合は、同じ可逆サイクルを複数個まとめて動作させて、それぞれの数を調整し、総計で同じ熱となるように調整する。（図2.11-右）。熱機関の効率の式(1.20) ${}^{\text{p.\ref{eq-EfficiencyEngine}}}$ と効率の関係の式(2.1) ${}^{\text{p.\ref{eq-InequalityRevCycleEfficiency}}}$ から

\frac{|W_{\mathrm{A}}|}{|Q_{\mathrm{H,A}}|}>\frac{|W_{\mathrm{B}}|}{|Q_{% \mathrm{H,B}}|}

ここで高温熱源とやりとりする熱が同じとなるように動作させている（ $|Q_{\mathrm{H,A}}|=|Q_{\mathrm{H,B}}|$ ）ので、次式が成り立つ。

\displaystyle|W_{\mathrm{A}}|>|W_{\mathrm{B}}|

(2.2)

上式と熱機関におけるエネルギー保存の式(1.22) ${}^{\text{p.\ref{eq-CycleEnergyConservation}}}$ とヒートポンプにおけるエネルギー保存の式(1.26) ${}^{\text{p.\ref{eq-CycleEnergyConservationPump}}}$ より、

|Q_{\mathrm{H,A}}|-|Q_{\mathrm{L,A}}|>|Q_{\mathrm{H,B}}|-|Q_{\mathrm{L,B}}|

高温熱源とやりとりする熱の大きさが同じになるように動作させている( $|Q_{\mathrm{H,A}}|=|Q_{\mathrm{H,B}}|$ )ので、次の関係が成り立つ。

\displaystyle|Q_{\mathrm{L,B}}|

\displaystyle>|Q_{\mathrm{L,A}}|

(2.3)

図2.11の右側の図のオレンジの点線のように高温熱源も含めた大きな一つの系として考えると、全体での仕事は式(2.2)より系から取り出されている（図2.11右の右側でオレンジの点線から外に出ている青の矢印）。また、低温熱源からの熱は式(2.3)より系が受け取っている（図2.11右の下側でオレンジの点線へ入っている赤の矢印）。高温熱源も含めた大きな系で見ると、系が低温熱源（一つの熱源）から熱を受け取り仕事に変換しているため、熱力学第二法則のトムソンの表現（2.2節 ${}^{\text{p.\ref{sec-2ndLawStatements}}}$ ）に反する ⁷⁷7クラウジウスの表現に反することを利用しても示すことができる。詳細は付録のB.7.1節 ${}^{\text{p.\ref{sec-RevCycleEfficiencyClausius}}}$ に示す。。よって、ある可逆サイクルの効率が他の可逆サイクルの効率よりも高くなることはありえない。すなわち同じ二つの熱源で動作する全ての可逆サイクルの効率は同じである。言い換えれば、二つの熱源が決まれば可逆サイクルの効率も決まる。

同じ効率の可逆サイクル

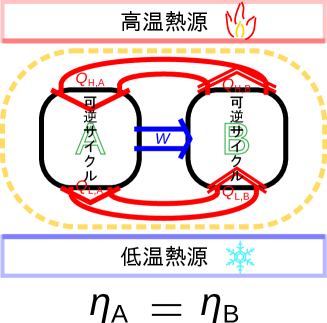
同じ効率の可逆サイクルであれば、図2.12ように可逆熱機関Aと可逆ヒートポンプBの熱源とやり取りする熱の量が等しく、全体として熱の移動がないと見なせるため熱力学第二法則に反しない。よって、同じ二つの熱源で動作する可逆サイクルは必ず同じ効率となる。

Figure 2.12: 効率の等しい可逆熱機関（可逆ヒートポンプ）

可逆サイクルの効率と不可逆の熱機関の効率

可逆サイクルの効率と不可逆の熱機関の効率を比較した場合、実在する不可逆の熱機関の効率が可逆サイクルの効率よりも高くなることはありえない（付録B.7.2 ${}^{\text{p.\ref{sec-ReversibleIrreversibleCycleEfficiency}}}$ に詳細を記している）。すなわち、可逆サイクルの熱機関としての効率は同じ二つの熱源を用いる中では最も高い。当然であるが可逆サイクルの熱機関としての効率が不可逆の熱機関よりも高い場合には熱力学第二法則に反することはない（付録B.7.3節 ${}^{\text{p.\ref{sec-ReversibleCycleEfficiencyApp}}}$ ）。また、可逆サイクルのヒートポンプとしての成績係数は、同じ二つの熱源を用いる実在する不可逆のヒートポンプよりも必ず高くなる（付録B.7.4節 ${}^{\text{p.\ref{sec-ReversibleIrreversibleCycleCOP}}}$ ）。実際の熱機関である自動車のエンジンでも、同じ熱源間⁸⁸8車のエンジンの高温熱源はガソリンの燃焼であり低温熱源は外気である。で働く可逆熱機関の効率を越えることは決して出来ない。ヒートポンプでも同じである⁹⁹9エアコンでの冷房では高温熱源は外気であり低温熱源は室内空気である。外気と室内空気を熱源とする可逆サイクルの成績係数は必ずどんな高性能なエアコンよりも高くなり、どんな可逆サイクルも同じ成績係数となる。。

2.4.4 可逆サイクルの熱と仕事と温度

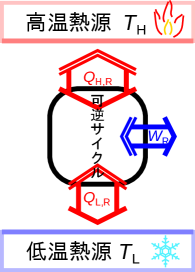
可逆サイクルの熱と仕事と温度の関係から、可逆サイクルの熱機関としての効率を明らかにする。先ほど示したように、同じ組み合わせの一定温度の熱源二つで動作する可逆サイクルは、どんな熱機関やヒートポンプでも必ず同じ効率となり構成によらない。すなわち、効率を決める要素は二つの熱源の条件だけであり、熱源と系（サイクル）は熱のやり取りしかなく、熱のやり取りに影響するのは温度のみである。つまり可逆サイクルの効率を決める条件は二つの熱源の温度の組み合わせのみである。よって温度 $T_{\mathrm{H}}$ [℃またはK]の熱源１と温度 $T_{\mathrm{L}}$ [℃またはK]の熱源２（ $T_{\mathrm{H}}>T_{\mathrm{L}}$ ）で動作する可逆サイクル（図2.13）の効率 $\eta_{可}$ は、この二つの熱源の温度（ $T_{\mathrm{H}}$ [℃またはK]、 $T_{\mathrm{L}}$ [℃またはK]）のみによって表される¹⁰¹⁰10可逆熱サイクルの効率が二つの熱源温度の組み合わせによらず一定であれば、この関数は温度によらない定数となる。。

Figure 2.13: 可逆サイクル

効率 $\eta_{可}$ と二つの熱源温度との関係 $f(T_{\mathrm{H}},T_{\mathrm{L}})$ は次式で表される。

\displaystyle\eta_{可}=f(T_{\mathrm{H}},T_{\mathrm{L}})

(2.4)

効率は仕事と高温熱源からの熱との比（式(1.20) ${}^{\text{p.\ref{eq-EfficiencyEngine}}}$ ）であるので、上式は次のように変形できる。

\displaystyle\frac{|W_{\mathrm{R}}|}{|Q_{\mathrm{H,R}}|}

\displaystyle=f(T_{\mathrm{H}},T_{\mathrm{L}})

(2.5)

ここで高温側の熱と低温側の熱の関係を求めるために、熱力学第一法則、次に示す式(1.22) ${}^{\text{p.\ref{eq-CycleEnergyConservation}}}$ を使う。

|Q_{\mathrm{H,R}}|=|Q_{\mathrm{L,R}}|+|W_{\mathrm{R}}|

この式を仕事 $W_{\mathrm{可}}$ を消すように(2.5)に代入し整理すると次式となる。

\displaystyle\frac{|Q_{\mathrm{L,R}}|}{|Q_{\mathrm{H,R}}|}

\displaystyle=1-f(T_{\mathrm{H}},T_{\mathrm{L}})

このように可逆サイクルの熱の比も温度の関数となる。右辺を $g(T_{\mathrm{H}},T_{\mathrm{L}})=1-f(T_{\mathrm{H}},T_{\mathrm{L}})$ とおきなおし次式を得る。

\displaystyle\frac{|Q_{\mathrm{L,R}}|}{|Q_{\mathrm{H,R}}|}=g(T_{\mathrm{H}},T_% {\mathrm{L}})

(2.6)

可逆サイクルの高温熱源からの熱と低温熱源からの熱の大きさの比は二つの熱源の温度のみの関数で表される。

2.4.5 三つの熱源での可逆サイクル

三つの熱源での可逆サイクルを考え、熱の比を表す関数 $g(T_{\mathrm{H}},T_{\mathrm{L}})$ がどのような関数か明らかにする。同じ組み合わせの熱源でなく異なる組み合わせの熱源で動作する可逆サイクルでの効率はどうなるだろうか。図2.14に示すように、温度 $T_{\mathrm{H}}$ [℃またはK]の熱源と温度 $T_{\mathrm{L}}$ [℃またはK]の熱源で動作する可逆サイクルAと、温度 $T_{\mathrm{H}}$ [℃またはK]の熱源と温度 $T_{\mathrm{M}}$ [℃またはK]の熱源で動作する可逆サイクルB、温度 $T_{\mathrm{M}}$ [℃またはK]の熱源と温度 $T_{\mathrm{L}}$ [℃またはK]の熱源で動作する可逆サイクルCを考える。このとき熱源の温度の関係は $T_{\mathrm{H}}>T_{\mathrm{M}}>T_{\mathrm{L}}$ とする。

Figure 2.14: 可逆熱機関の効率

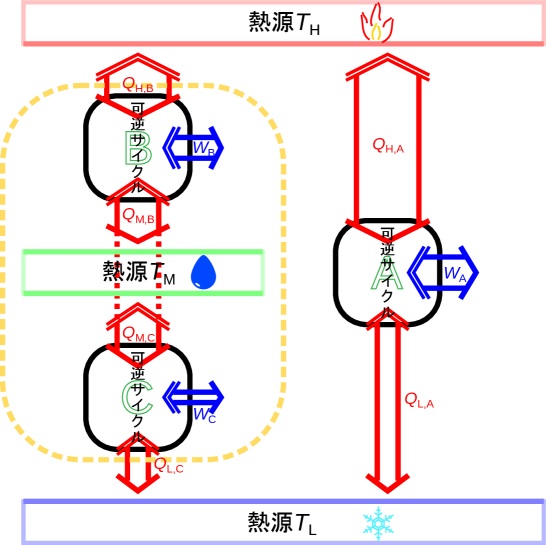
温度の関数 $g(T_{\mathrm{H}},T_{\mathrm{L}})$ を明らかにするため、それぞれの可逆サイクルと熱源との熱の大きさの関係を用いる。可逆サイクルBの低温側の熱源へ伝わる熱の大きさ $Q_{\mathrm{M,B}}$ [J]と、可逆サイクルCの高温側の熱源から伝わる熱の大きさ $Q_{\mathrm{M,C}}$ [J]を、同じ大きさ $Q_{\mathrm{M}}$ [J]になるよう ¹¹¹¹11 伝わる熱の大きさを同じにするように、可逆サイクルBと可逆サイクルCを複数個一緒に動作させ、それぞれの可逆サイクルの数を調整する。複数の可逆サイクルを一つの可逆サイクルとして考えれば、伝わる熱の大きさを等しくすることが出来る。にそれぞれの可逆熱機関を動作させて（ $|Q_{\mathrm{M,B}}|=|Q_{\mathrm{M,C}}|=|Q_{\mathrm{M}}|$ ）、図2.14の黄色の点線で示すように可逆サイクルBと可逆サイクルCを合わせて一つの可逆サイクルとして考える（黄色の点線で囲んだ合わせたサイクルは、温度 $T_{\mathrm{H}}$ の熱源と $Q_{\mathrm{H,B}}$ 、温度 $T_{\mathrm{L}}$ の熱源と $Q_{\mathrm{L,C}}$ の熱交換をしている）。可逆サイクルBと可逆サイクルCを合わせたサイクルと、可逆サイクルAは、ともに温度 $T_{\mathrm{H}}$ [℃またはK]と温度 $T_{\mathrm{L}}$ [℃またはK]の同じ二つの熱源の間で動作する可逆サイクルとみなせるので熱の比は等しく次式が成り立つ。この関係は三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つ。

\displaystyle\frac{|Q_{\mathrm{L,C可}}|}{|Q_{\mathrm{H,B可}}|}=\frac{|Q_{\mathrm% {L,A可}}|}{|Q_{\mathrm{H,A可}}|}

(2.7)

上式(2.7)の左辺の分子と分母に $|Q_{\mathrm{M可}}|$ をかけると次の関係が成り立つ。

\frac{|Q_{\mathrm{M可}}|}{|Q_{\mathrm{H,B可}}|}\frac{|Q_{\mathrm{L,C可}}|}{|Q_{% \mathrm{M可}}|}=\frac{|Q_{\mathrm{L,A可}}|}{|Q_{\mathrm{H,A可}}|}

上式左辺は可逆サイクルBの熱の比と可逆サイクルCの熱の比の積と同じ形になった。右辺は可逆サイクルAの熱の比であるので、両辺をそれぞれ温度の関数 $g$ （式(2.6)）で次式のように表す事ができる¹²¹²12ここで関数 $g$ （関数 $f$ ）が温度によらず一定であると成り立たないため、関数 $g$ （関数 $f$ ）は定数ではない。。

\displaystyle g(T_{\mathrm{H}},T_{\mathrm{M}})g(T_{\mathrm{M}},T_{\mathrm{L}})% =g(T_{\mathrm{H}},T_{\mathrm{L}})

(2.8)

この関係は三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つことから関数 $g$ がどのような関数かを考える。上式(2.8)で、左辺は $T_{\mathrm{M}}$ [℃またはK]を含む関数となっているが、右辺は $T_{\mathrm{H}}$ [℃またはK]と $T_{\mathrm{L}}$ [℃またはK]のみの関数で $T_{\mathrm{M}}$ [℃またはK]を含んでいない。三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つためには、関数 $g$ は左辺の積の計算で $T_{\mathrm{M}}$ [℃またはK]が消える形の関数である必要がある。

もし、関数 $g$ が次のような形であったらどうなるか、試しに計算をしてみよう。

\displaystyle g(T_{\mathrm{H}},T_{\mathrm{L}})=T_{\mathrm{L}}+T_{\mathrm{H}}

(2.9)

元の式(2.8)の $g$ に入れてみる。

	$\displaystyle g(T_{\mathrm{H}},T_{\mathrm{M}})g(T_{\mathrm{M}},T_{\mathrm{L}})$	$\displaystyle=g(T_{\mathrm{H}},T_{\mathrm{L}})$
	$\displaystyle(T_{\mathrm{M}}+T_{\mathrm{H}})(T_{\mathrm{L}}+T_{\mathrm{M}})$	$\displaystyle=T_{\mathrm{L}}+T_{\mathrm{H}}$
	$\displaystyle T_{\mathrm{L}}T_{\mathrm{M}}+T_{\mathrm{L}}T_{\mathrm{H}}+T_{% \mathrm{M}}^{2}+T_{\mathrm{M}}T_{\mathrm{H}}$	$\displaystyle=T_{\mathrm{L}}+T_{\mathrm{H}}$
	$\displaystyle T_{\mathrm{L}}T_{\mathrm{M}}+T_{\mathrm{L}}T_{\mathrm{H}}-T_{% \mathrm{L}}$	$\displaystyle=-T_{\mathrm{M}}^{2}-T_{\mathrm{M}}T_{\mathrm{H}}+T_{\mathrm{H}}$
	$\displaystyle T_{\mathrm{L}}$	$\displaystyle=\frac{-T_{\mathrm{M}}^{2}-T_{\mathrm{M}}T_{\mathrm{H}}+T_{% \mathrm{H}}}{T_{\mathrm{M}}+T_{\mathrm{H}}-1}$

上式の関係であると $T_{\mathrm{L}}$ が $T_{\mathrm{M}}$ と $T_{\mathrm{H}}$ の関数になっており、任意のはずの $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ が上式の関係となる熱源温度でしか成り立たず、式(2.9)の形の関数 $g$ は間違った形であったことがわかる。

左辺の積の計算で $T_{\mathrm{M}}$ [℃またはK]が消えるためには、関数 $g$ が割り算で表される形がある。一番簡単な形として次の形が考えられる。

\displaystyle g(T_{\mathrm{H}},T_{\mathrm{L}})=\frac{T_{\mathrm{L}}}{T_{% \mathrm{H}}}

(2.10)

元の式(2.8)の $g$ に入れてみる。

	$\displaystyle g(T_{\mathrm{H}},T_{\mathrm{M}})g(T_{\mathrm{M}},T_{\mathrm{L}})$	$\displaystyle=g(T_{\mathrm{H}},T_{\mathrm{L}})$
	$\displaystyle\frac{T_{\mathrm{M}}}{T_{\mathrm{H}}}\frac{T_{\mathrm{L}}}{T_{% \mathrm{M}}}$	$\displaystyle=\frac{T_{\mathrm{L}}}{T_{\mathrm{H}}}$
	$\displaystyle\frac{T_{\mathrm{L}}}{T_{\mathrm{H}}}$	$\displaystyle=\frac{T_{\mathrm{L}}}{T_{\mathrm{H}}}$

上式は左辺と右辺が同じになっているので、三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つ。関数 $g$ が式(2.10)の形であれば元の式(2.8)が三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つことがわかる。

関数 $g$ が他の割り算の形でも成り立つ。例えばとして次の形を考えてみる。

\displaystyle g(T_{\mathrm{H}},T_{\mathrm{L}})=\frac{3T_{\mathrm{L}}+20}{3T_{% \mathrm{H}}+20}

(2.11)

元の式(2.8)の $g$ に入れてみる。

	$\displaystyle g(T_{\mathrm{H}},T_{\mathrm{M}})g(T_{\mathrm{M}},T_{\mathrm{L}})$	$\displaystyle=g(T_{\mathrm{H}},T_{\mathrm{L}})$
	$\displaystyle\frac{3T_{\mathrm{M}}+20}{3T_{\mathrm{H}}+20}\;\frac{3T_{\mathrm{% L}}+20}{3T_{\mathrm{M}}+20}$	$\displaystyle=\frac{3T_{\mathrm{L}}+20}{3T_{\mathrm{H}}+20}$
	$\displaystyle\frac{3T_{\mathrm{L}}+20}{3T_{\mathrm{H}}+20}$	$\displaystyle=\frac{3T_{\mathrm{L}}+20}{3T_{\mathrm{H}}+20}$

上式は左辺と右辺が同じになっているので、三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つ。関数 $g$ が式(2.11)の形であれば元の式(2.8)が三つの熱源の温度（ $T_{\mathrm{H}}$ 、 $T_{\mathrm{M}}$ 、 $T_{\mathrm{L}}$ ）がどのような値になっても必ず成り立つことがわかる。

関数 $g$ を割り算の形にした式(2.10)と式(2.11)は、分子と分母がそれぞれ一つの温度に対して同じ形の関数となっている。一つの温度に対する関数は他の形でも成り立ちそうであるので、ある関数 $\phi(T)$ と置いた次式で表される関数 $g$ で考えてみる。

\displaystyle g(T_{\mathrm{H}},T_{\mathrm{L}})=\frac{\phi(T_{\mathrm{L}})}{% \phi(T_{\mathrm{H}})}

(2.12)

上式のように関数 $g$ が温度の商の関数だと、次式のように $T_{\mathrm{M}}$ [℃またはK]が左辺から消える。

g(T_{\mathrm{H}},T_{\mathrm{M}})g(T_{\mathrm{M}},T_{\mathrm{L}})=\frac{\phi(T_% {\mathrm{M}})}{\phi(T_{\mathrm{H}})}\frac{\phi(T_{\mathrm{L}})}{\phi(T_{% \mathrm{M}})}=\frac{\phi(T_{\mathrm{L}})}{\phi(T_{\mathrm{H}})}=g(T_{\mathrm{H% }},T_{\mathrm{L}})

このように関数 $g$ が温度の商の関数であると言える。熱源の温度と、熱源とやりとりする熱量の関係をまとめると式(2.6)と式(2.12)より次式が成り立つ。

\displaystyle\frac{|Q_{\mathrm{L可}}|}{|Q_{\mathrm{H可}}|}=\frac{\phi(T_{\mathrm% {L}})}{\phi(T_{\mathrm{H}})}

(2.13)

2.4.6 熱力学的温度と可逆サイクルの効率

熱力学的温度と可逆サイクルの効率の関係をより詳しく見ていく。前節の $\phi(T)$ （式(2.13)）をSI（国際単位系）では基本単位である熱力学的温度（絶対温度） $\varTheta$ （単位はK(ケルビン)）として定義されている[23][22]¹³¹³13熱力学的温度（絶対温度）の詳細は3.2節 ${}^{\text{p.\ref{sec-Temperature}}}$ に記す。

\varTheta=\phi(T)

また日常使われる摂氏温度 $\theta$ [℃]は国際的にSI（国際単位系）の組立単位として絶対温度 $\varTheta$ [K]により次式で定義されている[22] ¹⁴¹⁴14関数 $\phi$ と摂氏温度 $\theta$ [℃]の関係は次式で表される。 $\theta+273.15=\phi(T)$ 。

\varTheta=\theta+273.15

この熱力学的温度で表現すると、温度 $\varTheta_{\mathrm{H}}$ [K]と温度 $\varTheta_{\mathrm{L}}$ [K]の二つの熱源で動作する可逆熱機関の熱源とやりとりする熱量 $Q_{\mathrm{H}}$ [J]と熱量 $Q_{\mathrm{L}}$ [J]の関係は次のように熱力学的温度（絶対温度）の比で表される ¹⁵¹⁵15 関数 $g(T_{\mathrm{H}},T_{\mathrm{L}})$ は次のように表される。 $\displaystyle\frac{|Q_{\mathrm{L可}}|}{|Q_{\mathrm{H可}}|}=\frac{\varTheta_{% \mathrm{L}}}{\varTheta_{\mathrm{H}}}$ $\displaystyle=g(T_{\mathrm{H}},T_{\mathrm{L}})$ 。

\displaystyle\frac{|Q_{\mathrm{L可}}|}{|Q_{\mathrm{H可}}|}=\frac{\varTheta_{% \mathrm{L}}}{\varTheta_{\mathrm{H}}}

(2.15)

変形し次式の様に表すこともできる ¹⁶¹⁶16絶対値を外すと $Q_{\mathrm{H}}$ [J]と $Q_{\mathrm{L}}$ [J]は熱機関（ヒートポンプ）に対し入る向きと出る向きと伝わる方向が逆であり、符号が逆となるので次式となる。 $\displaystyle\frac{Q_{\mathrm{H可}}}{\varTheta_{\mathrm{H}}}=-\frac{Q_{\mathrm{% L可}}}{\varTheta_{\mathrm{L}}}$ 。

\displaystyle\frac{|Q_{\mathrm{H可}}|}{\varTheta_{\mathrm{H}}}=\frac{|Q_{% \mathrm{L可}}|}{\varTheta_{\mathrm{L}}}

(2.16)

式(1.24) ${}^{\text{p.\ref{eq-EfficiencyEngineQ}}}$ と式(2.15)より、温度 $\varTheta_{\mathrm{H}}$ [K]の熱源と温度 $\varTheta_{\mathrm{L}}$ [K]の熱源（ $\varTheta_{\mathrm{H}}>\varTheta_{\mathrm{L}}$ ）で動作する可逆熱機関の効率は次式(2.17)で表される ¹⁷¹⁷17 関数 $f(T_{\mathrm{H}},T_{\mathrm{L}})$ は次のように表される。 $\displaystyle\frac{|W_{\mathrm{可}}|}{|Q_{\mathrm{H可}}|}=\frac{\varTheta_{% \mathrm{H}}-\varTheta_{\mathrm{L}}}{\varTheta_{\mathrm{H}}}=f(T_{\mathrm{H}},T% _{\mathrm{L}})$ 。

$\displaystyle\eta_{\mathrm{HL可}}$	$\displaystyle=\frac{\|Q_{\mathrm{H可}}\|-\|Q_{\mathrm{L可}}\|}{\|Q_{\mathrm{H可}}\|}$
	$\displaystyle=1-\frac{\|Q_{\mathrm{L可}}\|}{\|Q_{\mathrm{H可}}\|}$
	$\displaystyle=1-\frac{\varTheta_{\mathrm{L}}}{\varTheta_{\mathrm{H}}}$
	$\displaystyle=\frac{\varTheta_{\mathrm{H}}-\varTheta_{\mathrm{L}}}{\varTheta_{% \mathrm{H}}}$	(2.17)

2.4.7 問題

問題をいくつかあげる。

1.

熱源として5 ℃（深層の海水の温度）、20 ℃（大気の温度）、100℃（沸騰しているお湯の温度）、1000℃（燃焼の温度）がある。この中で可逆熱機関を動作させた際に最も効率の高くなる熱源の組み合わせはどれか。また、効率を求めよ。
2.

1000℃の高温熱源から900℃の低温熱源へ熱が伝わっている間で可逆熱機関を動作させた場合と、高温熱源100℃から低温熱源0℃へ熱が伝わっている間で可逆熱機関を動作させた場合を考える。どちらの場合も熱源間の温度差は100℃である。この時、それぞれの可逆熱機関の効率を求めよ。
3.

300 Kの地球表面で2.7 Kの何もない宇宙空間[6]との間と、約6000 Kの太陽表面[14]との間でそれぞれ可逆熱機関を動作させた際の効率を求めよ（熱源温度に地球表面温度、宇宙空間の温度、太陽の表面温度を用いる）。
4.

式(1.27) ${}^{\text{p.\ref{eq-EfficiencyPumpQ}}}$ と式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ より温度 $\varTheta_{\mathrm{1}}$ [K]の熱源と温度 $\varTheta_{\mathrm{2}}$ [K]の熱源（ $\varTheta_{\mathrm{1}}>\varTheta_{\mathrm{2}}$ ）で動作する可逆ヒートポンプの成績係数を示せ。
5.

低温熱源が0 Kであり、高温熱源が300 Kである場合に、可逆熱機関と可逆ヒートポンプを動作させた際の効率と成績係数を求めよ。

2.4.8 解答

解答を示す。

1.

可逆熱機関の効率は式(2.17) ${}^{\text{p.\ref{eq-CarnotHeatengineEfficiency}}}$ で表される。二つの熱源の差が大きいほど効率は良くなるため、5℃と1000℃の組み合わせが最も効率が高くなる。式(2.17)中 $\varTheta_{\mathrm{1}}$ [K]が高温熱源温度、 $\varTheta_{\mathrm{2}}$ [K]が低温熱源の温度であるので、それぞれの値を求める。

$\displaystyle\varTheta_{\mathrm{1}}$ $\displaystyle=1000\>\mathrm{\textcelsius}+273.15=1273.15\>\mathrm{K}$

$\displaystyle\varTheta_{\mathrm{2}}$ $\displaystyle=5\>\mathrm{\textcelsius}+273.15=278.15\>\mathrm{K}$

$\eta=\frac{\varTheta_{\mathrm{1}}-\varTheta_{\mathrm{2}}}{\varTheta_{\mathrm{1% }}}=\frac{1273.15\>\mathrm{K}-278.15\>\mathrm{K}}{1273.15\>\mathrm{K}}\simeq 0% .781$

効率は0.781である。
2.

可逆熱機関の効率は式(2.17) ${}^{\text{p.\ref{eq-CarnotHeatengineEfficiency}}}$ で表される。 1000℃と900℃の組合せでの効率 $\eta_{\mathrm{h}}$ は次のように求められる。

$\eta_{\mathrm{h}}=\frac{1273.15\>\mathrm{K}-1173.15\>\mathrm{K}}{1273.15\>% \mathrm{K}}\simeq 0.079$

100℃と0℃の組合せでの効率 $\eta_{\mathrm{l}}$ は次のように求められる。

$\eta_{\mathrm{l}}=\frac{373.15\>\mathrm{K}-273.15\>\mathrm{K}}{373.15\>\mathrm% {K}}\simeq 0.268$

このように同じ温度差で可逆熱機関を動作させた場合でも、熱源の温度によって効率は大きく異なる。 900℃の低温熱源で効率0.268を得るには1130.14℃の高温熱源が必要である。
3.

可逆熱機関の効率は式(2.17) ${}^{\text{p.\ref{eq-CarnotHeatengineEfficiency}}}$ で表される。何もない宇宙空間との組合せでの効率 $\eta_{\mathrm{space}}$ は次のように求められる。

$\eta_{\mathrm{space}}=\frac{300\>\mathrm{K}-2.7\>\mathrm{K}}{300\>\mathrm{K}}% \simeq 0.991$

太陽との組合せでの効率 $\eta_{\mathrm{sun}}$ は次のように求められる。

$\eta_{\mathrm{sun}}=\frac{6000\>\mathrm{K}-300\>\mathrm{K}}{6000\>\mathrm{K}}% \simeq 0.950$

このように宇宙空間と地球表面での方が効率が高いが、伝わる熱量は太陽からの方が圧倒的に大きいため、動作させれば得られる仕事は太陽との方が大きくなる。
4.

可逆ヒートポンプの成績係数は式(1.27) ${}^{\text{p.\ref{eq-EfficiencyPumpQ}}}$ より

$\epsilon_{\mathrm{12可}}=\frac{|Q_{\mathrm{1可}}|}{|Q_{\mathrm{1可}}|-|Q_{\mathrm% {2可}}|}=\frac{1}{1-\dfrac{|Q_{\mathrm{2可}}|}{|Q_{\mathrm{1可}}|}}$

ここに式(2.15) ${}^{\text{p.\ref{eq-AbsoluteTemperature}}}$ を代入する。

$\epsilon_{\mathrm{12可}}=\frac{1}{1-\dfrac{\varTheta_{\mathrm{2}}}{\varTheta_{% \mathrm{1}}}}=\frac{\varTheta_{\mathrm{1}}}{\varTheta_{\mathrm{1}}-\varTheta_{% \mathrm{2}}}$

可逆ヒートポンプの成績係数は熱源の温度により上式のように表される。
5.

可逆熱機関の効率は式(2.17) ${}^{\text{p.\ref{eq-CarnotHeatengineEfficiency}}}$ で表される。 0 Kと300 Kの組み合わせでの効率 $\eta_{\mathrm{0K}}$ は次のように求められる。

$\eta_{\mathrm{0K}}=\frac{300\>\mathrm{K}-0\>\mathrm{K}}{300\>\mathrm{K}}=1$

このように低温熱源が0 Kである場合には高温熱源の温度にかかわらず効率は1となり、高温熱源から受け取った熱は全て仕事に変換できる。次に可逆ヒートポンプの成績係数は上問の解答より成績係数 $\epsilon_{\mathrm{0K}}$ は次のように求められる。

$\epsilon_{\mathrm{0K}}=\frac{300\>\mathrm{K}}{300\>\mathrm{K}-0\>\mathrm{K}}=1$

このように低温熱源が0 Kである場合には高温熱源の温度にかかわらず可逆ヒートポンプの成績係数は1となり、高温側で得られる熱は仕事からのみであり、低温熱源から熱を奪うことはできない。

2.3 可逆な変化 References 2.5 エントロピー

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。

	$\displaystyle\varTheta_{\mathrm{1}}$	$\displaystyle=1000\>\mathrm{\textcelsius}+273.15=1273.15\>\mathrm{K}$
	$\displaystyle\varTheta_{\mathrm{2}}$	$\displaystyle=5\>\mathrm{\textcelsius}+273.15=278.15\>\mathrm{K}$