


Next: 2.4.4.1 圧縮性流体(密度 [kg/m ]は変化する)
Up: 2.4 エネルギー保存
Previous: 2.4.3 時間あたりに伝わる熱
2.4.4 時間あたりの仕事
時間あたりの仕事(仕事率)は面に作用する力と速度の内積で表される2.6。面に作用する力は図2.5を参照(p. ![[*]](crossref.png) )。コントロールボリュームのそれぞれの面について考える。その際、展開後に微分の四乗となる項
)。コントロールボリュームのそれぞれの面について考える。その際、展開後に微分の四乗となる項
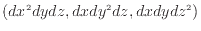 は十分に小さいため無視する。
は十分に小さいため無視する。
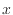 軸に垂直
軸に垂直 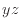 面左
面左-
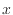 軸に垂直
軸に垂直 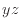 面右
面右-
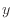 軸に垂直
軸に垂直 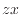 面下
面下-
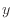 軸に垂直
軸に垂直 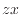 面上
面上-
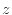 軸に垂直
軸に垂直 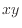 面後
面後-
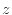 軸に垂直
軸に垂直 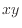 面前
面前-
各面にかかる力はコントロールボリュームから出る方向を正としているので、符号をあわせて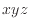 軸に垂直な面それぞれ足し合わせる。その和が“時間あたりの仕事"になる。
軸に垂直な面それぞれ足し合わせる。その和が“時間あたりの仕事"になる。
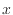 軸に垂直面
軸に垂直面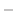 式(2.166)
式(2.166)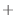 式(2.167)
式(2.167)
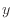 軸に垂直面
軸に垂直面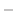 式(2.168)
式(2.168)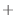 式(2.169)
式(2.169)
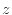 軸に垂直面
軸に垂直面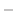 式(2.170)
式(2.170)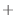 式(2.171)
式(2.171)
ここで、式(2.60)で表される面に垂直な応力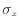 、
、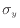 、
、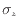 [Pa]を圧力と粘性力の項に分け、次のように表す。
[Pa]を圧力と粘性力の項に分け、次のように表す。
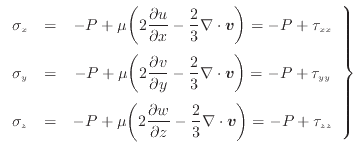 |
(2.174) |
式(2.172)、式(2.173)、式(2.174)の和に上式の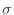 を代入すると、次式となる。ここで、コントロールボリュームの体積(
を代入すると、次式となる。ここで、コントロールボリュームの体積(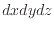 )で括られている項の中での各境界面での区別はしない(2.1.7節 p.
)で括られている項の中での各境界面での区別はしない(2.1.7節 p.![[*]](crossref.png) )。
)。
Subsections



Next: 2.4.4.1 圧縮性流体(密度 [kg/m ]は変化する)
Up: 2.4 エネルギー保存
Previous: 2.4.3 時間あたりに伝わる熱
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![[*]](crossref.png) )。コントロールボリュームのそれぞれの面について考える。その際、展開後に微分の四乗となる項
)。コントロールボリュームのそれぞれの面について考える。その際、展開後に微分の四乗となる項
![]() 軸に垂直な面それぞれ足し合わせる。その和が“時間あたりの仕事"になる。
軸に垂直な面それぞれ足し合わせる。その和が“時間あたりの仕事"になる。
![]() 、
、![]() 、
、![]() [Pa]を圧力と粘性力の項に分け、次のように表す。
[Pa]を圧力と粘性力の項に分け、次のように表す。
![[*]](crossref.png) )。
)。