2 熱力学第二法則とエントロピー 2.4 可逆サイクル（可逆熱機関・可逆ヒートポンプ）の効率と熱力学的温度 2.6 ヘルムホルツの自由エネルギー

2.5 エントロピー

エントロピーを不可逆の指標となるように定義する。これまで不可逆と熱力学第二法則についてみてきたが、不可逆性を数値的にエントロピーによって表せるようにしていこう。

2.5.1 エントロピーの条件

エントロピーの条件を、全体として断熱された系において不可逆の指標となる状態量となるようにしたい¹⁸¹⁸18以下のエントロピーの定義の導出はイメージのしやすさを優先しているため、厳密な考え方については他の熱力学の教科書[1][19]等で確認するとよい。。すなわち、熱力学第二法則（2節 ${}^{\text{p.\ref{sec-2ndLaw}}}$ ）が時間の流れの方向を示したように、時間の流れる方向を数値で表す指標とする。時間が流れる方向の変化に対して断熱された系ではエントロピーが増大するように定義したい ¹⁹¹⁹19複雑な現象で、次にどちらの方向に現象が動いていくのかがすぐには分からない場合に、どちらに動くか判断する指標となる。。そこで次の三つの条件が成り立つようにエントロピーを定義する（全体として断熱されていることが大前提である）。

条件1

断熱された一つの系での”可逆”の変化では（仕事の作用があっても）、どちらに時間が流れてもよいので、エントロピーは変化しない。

条件2

断熱された一つの系の状態が変化した際、不可逆の変化であれば時間の経過でエントロピーが増加する。

条件3

全体は断熱された内部に複数の系が存在する場合、それぞれの系の間では熱のやりとりがある場合でも全体では条件1（条件3-1）と条件2（条件3-2）が成り立つ。

条件3-1: 全体は断熱された内部に複数の系がある場合において、可逆の変化では合計のエントロピーは変化しない。
条件3-2: 全体は断熱された内部に複数の系がある場合において、不可逆の変化では時間の経過でエントロピーが増加する。

2.5.2 条件からの検討

条件からの検討をしていく。条件1で示したように断熱された系が可逆変化した場合、エントロピー $S$ は変化しないように定義したい。可逆断熱変化でのエントロピーの変化を $\mathrm{d}S_{\mathrm{可逆断熱}}$ とすると条件1は次式で表される。

\displaystyle\mathrm{d}S_{\mathrm{可逆断熱}}=0

(2.18)

条件2の不可逆の変化で増加する性質を考える。時間の流れる方向での変化でエントロピーが増加し、逆の時間の流れだと減少するようにする。断熱された一つの系で、熱が発生する場合は現象は不可逆となる（2.2.3節 ${}^{\text{p.\ref{sec-HeatIrreversibility}}}$ ）。そこで、発熱する場合にエントロピーが増えるように定義する。これまでに発熱をする場合には熱 $Q$ は正と定義しているので、それに対応するエントロピーの変化量も正とするように条件2は次のように表す。

\displaystyle Q>0\quad のとき\quad\mathrm{d}S>0

(2.19)

上の式(2.18)と式(2.19)の関係を満たすエントロピーの形の候補として、 2.4.6節 ${}^{\text{p.\ref{sec-AbsoluteTemperature}}}$ で可逆サイクルの関係で出てきた「 $Q/\varTheta$ 」が考えられる。この「 $Q/\varTheta$ 」が、条件3の全体として断熱された内部に複数の系があり内部で熱のやり取りのある系の場合に条件を満たすか、一つの熱源とサイクルを含む系、二つの熱源とサイクルを含む系、複数の熱源とサイクルを含む系について検討していく。

2.5.3 一つの熱源とサイクル（二つの系）

一つの熱源とサイクル（二つの系）が全体で断熱された中にあるとき、熱力学第二法則トムソンの表現に合う系と反する系でのエントロピーの定義として「 $Q/\varTheta$ 」が前に示した条件3-2（全体でエントロピーが増加する）と合うかを考える。

熱力学第二法則トムソンの表現に合う系

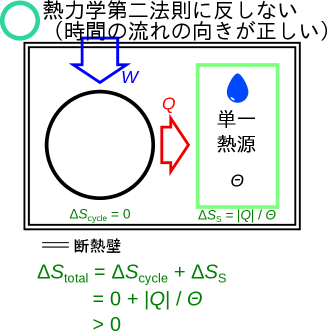
熱力学第二法則トムソンの表現に合う系を考える。図2.15のように、全体で断熱された系の中に、単一熱源系（温度 $\varTheta$ ）と仕事を熱に変換するサイクルである系（摩擦など簡単に実現できる）の二つの系がある場合は熱力学第二法則トムソンの表現に合う。ここでエントロピーを $Q/\varTheta$ として計算をしてみよう。サイクルは一サイクルの初めと終わりの状態が変わらないため状態は変化しない。エントロピーも一サイクルの始めと終わりで同じ状態となるため、可逆サイクルを含む全てのサイクルは一サイクル中でエントロピーは変化しない（ $\Delta S_{\mathrm{cycle}}=0$ ） ²⁰²⁰20ここまでの仮定ではサイクルでエントロピーが変化しないことを示すことが出来ないが、エントロピーのイメージをつかんでもらうために、ここではサイクルでのエントロピーは変化しないものとする。ここでのサイクルでは仕事から熱に変換されることで増えるエントロピーと熱源へ熱を伝えることで減るエントロピーが等しい。。単一熱源系は熱を受け取るので熱は正となり $\Delta S_{\mathrm{S}}=|Q|/\varTheta_{\mathrm{H}}$ となる。サイクルと熱源の二つの系があり、どちらに伝わる熱と考えるかで $Q$ の符号が変わるため、複数の系の場合は絶対値をつけ $|Q|$ とし、正か負かわかりやすいように表現をする。単一熱源系でエントロピーは増加し、全体での変化量 $\Delta S_{\mathrm{total}}$ は次のようになる。

	$\displaystyle\Delta S_{\mathrm{total}}$	$\displaystyle=\Delta S_{\mathrm{cycle}}+\Delta S_{\mathrm{S}}$
		$\displaystyle=0+\frac{\|Q\|}{\varTheta_{\mathrm{H}}}$
		$\displaystyle>0$

熱力学第二法則トムソンの表現にあう「時間の流れが正しい方向に流れている」場合に、全体でエントロピーは増加をしていることがわかる。正しい時間の向きでエントロピーが増加したので、エントロピーとして $Q/\varTheta$ を用いることはここの条件では目的にかなっている。

Figure 2.15: 熱源とトムソンの表現

熱力学第二法則トムソンの表現に反する系

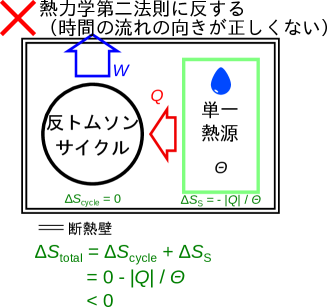
熱力学第二法則トムソンの表現に反する系を考える。図2.16のように、全体で断熱された系の中に、単一熱源系（温度 $\varTheta$ ）と単一熱源からの熱を仕事に変換する反トムソンサイクルの系の二つの系がある場合を考える。ここでもエントロピーを $Q/\varTheta$ として計算をしてみよう。単一熱源系は熱を渡しているので熱は負であり次式のように求められる。

	$\displaystyle\Delta S_{\mathrm{S}}$	$\displaystyle=-\frac{\|Q\|}{\varTheta_{\mathrm{H}}}$
		$\displaystyle<0$

サイクルはエントロピーは変わらないため、全体で減少する。

	$\displaystyle\Delta S_{\mathrm{total}}$	$\displaystyle=\Delta S_{\mathrm{cycle}}+\Delta S_{\mathrm{S}}$
		$\displaystyle=0-\frac{\|Q\|}{\varTheta_{\mathrm{H}}}$
		$\displaystyle<0$

熱力学第二法則トムソンの表現に反する「時間の流れが正しい方向に流れていない」場合に、全体でエントロピーが減少している。ここからも $Q/\varTheta$ がエントロピーの定義としてふさわしいことがわかる。

Figure 2.16: 熱源と反トムソンサイクル

2.5.4 二つの熱源とサイクル（三つの系）

二つの熱源とサイクル（三つの系）が全体で断熱された系の中にある場合に、可逆サイクル、熱力学第二法則クラウジウスの表現に合うサイクル、熱力学第二法則クラウジウスの表現に反するサイクルが含まれる系についてそれぞれ考えていく。

可逆サイクル

可逆サイクルが含まれる場合の、条件3-1（系全体で条件1「可逆では変化しない」が成り立つ）を考える。可逆サイクルと高温熱源の系、低温熱源の系があり、図2.17のように全体として断熱されている系を考える。この系は全体で断熱されていて可逆サイクルが可逆変化をするため、全体でエントロピーが変化しないような定義にしたい。

Figure 2.17: 熱源と可逆サイクル

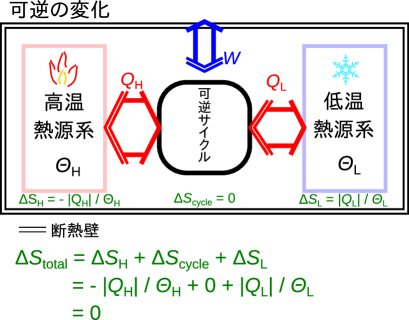
全体としてのエントロピーの変化（ $\Delta S_{\mathrm{total}}$ ）は次式のように各系のエントロピー変化の和を求めればよい（高温熱源のエントロピー変化は $\Delta S_{\mathrm{H}}$ 、低温熱源のエントロピー変化は $\Delta S_{\mathrm{L}}$ 、可逆サイクルのエントロピー変化は $\Delta S_{\mathrm{cycle}}$ ）。

\displaystyle\Delta S_{\mathrm{total}}=\Delta S_{\mathrm{H}}+\Delta S_{\mathrm% {cycle}}+\Delta S_{\mathrm{L}}

(2.20)

この中で、サイクルはエントロピーは変化しない。よって次式が成り立つ。

\displaystyle\Delta S_{\mathrm{cycle}}=0

(2.21)

熱源でのエントロピーの変化を可逆サイクルが熱機関として動いた熱の流れで考える（逆のヒートポンプで動作した場合には高温熱源と低温熱源の双方の符号を逆にすれば同じ結果が得られる）。可逆熱機関であれば高温熱源は熱が出ていくので熱は負の値となり、次式で表される。

\displaystyle\Delta S_{\mathrm{H}}=-\frac{|Q_{\mathrm{H}}|}{\varTheta_{\mathrm% {H}}}

(2.22)

低温熱源は熱を受け取るので熱は正の値となり、次式で表される。

\displaystyle\Delta S_{\mathrm{L}}=\frac{|Q_{\mathrm{L}}|}{\varTheta_{\mathrm{% L}}}

(2.23)

可逆サイクルでの熱と温度の関係は、式(2.16) ${}^{\text{p.\ref{eq-CarnotHeatTemp}}}$ より以下の関係がえられる。

\displaystyle-\frac{|Q_{\mathrm{H}}|}{\varTheta_{\mathrm{H}}}+\frac{|Q_{% \mathrm{L}}|}{\varTheta_{\mathrm{L}}}=0

(2.24)

式(2.20)へ式(2.21)、式(2.22)、式(2.23)、式(2.24)を代入すると、高温熱源での増加分と低温熱源での減少分が等しく、系全体のエントロピーの変化はゼロとなることが分かる。

	$\displaystyle\Delta S_{\mathrm{total}}$	$\displaystyle=\Delta S_{\mathrm{H}}+\Delta S_{\mathrm{cycle}}+\Delta S_{% \mathrm{L}}$
		$\displaystyle=0$

つまり $Q/\varTheta$ をエントロピーとすると、可逆の過程で断熱された系では変化しない量となる。

正しい時間の流れ（熱力学第二法則に反しない）

正しい時間の流れ（熱力学第二法則に反しない）ではエントロピーが増加する条件3-2（全体で条件2が成り立つ）を考える。熱力学第二法則（2.2節 ${}^{\text{p.\ref{sec-2ndLawStatements}}}$ ）に合う場合には「時間の流れも正しい方向に流れている」と言えるためエントロピーが増加することを確認する。熱力学第二法則クラウジウスの表現に合う通常身の回りでおこりうる現象として、高温から低温へ熱を伝える系を考える。図2.18のように、全体で断熱された系の中に、高温熱源系（温度 $\varTheta_{\mathrm{H}}$ ）、低温熱源系（温度 $\varTheta_{\mathrm{L}}$ ）、高温から低温に熱 $Q$ を伝えるだけのサイクルの系の三つの系がある場合は、サイクルを介して高温から低温に熱が伝わっているだけなので、熱力学第二法則クラウジウスの表現に合う。

Figure 2.18: エントロピーとクラウジウスの表現

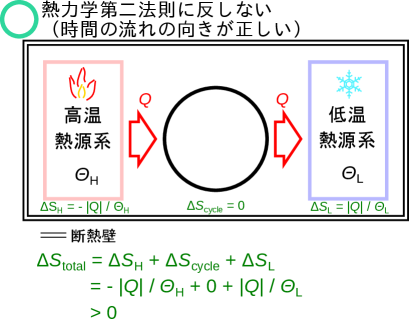
ここでもエントロピーを先ほどのように $Q/\varTheta$ として計算をしてみよう。間のサイクルは同じ状態で動作するのでエントロピーは変化しない。高温熱源系は熱を与えるので熱は負となり $\Delta S_{\mathrm{H}}=-|Q|/\varTheta_{\mathrm{H}}$ となる。低温熱源系は熱を受け取るので熱は正となり $\Delta S_{\mathrm{L}}=|Q|/\varTheta_{\mathrm{L}}$ となる。高温熱源系でエントロピーは減少し、低温熱源系でエントロピーは増加する。全体での変化量 $\Delta S_{\mathrm{total}}$ は次のようになる。

	$\displaystyle\Delta S_{\mathrm{total}}$	$\displaystyle=\Delta S_{\mathrm{H}}+\Delta S_{\mathrm{cycle}}+\Delta S_{% \mathrm{L}}$
		$\displaystyle=\frac{-\|Q\|}{\varTheta_{\mathrm{H}}}+0+\frac{\|Q\|}{\varTheta_{% \mathrm{L}}}$
		$\displaystyle=\|Q\|\left(-\frac{1}{\varTheta_{\mathrm{H}}}+\frac{1}{\varTheta_{% \mathrm{L}}}\right)>0$

温度は高温熱源系が低温熱源系よりも高い（ $\varTheta_{\mathrm{H}}>\varTheta_{\mathrm{L}}$ ）ため、全体でエントロピーは増加をしていることがわかる。正しい時間の向きでエントロピーが増加したので、エントロピーとして $Q/\varTheta$ を用いることはここの条件では目的にかなっている。

正しくない時間の流れ（熱力学第二法則に反する）

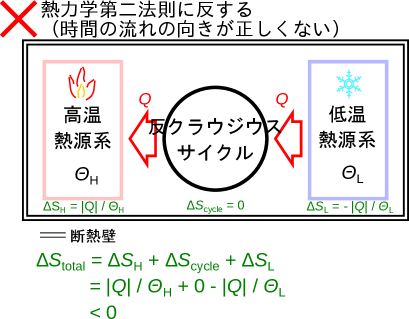
正しくない時間の流れ（熱力学第二法則に反する）では時間の流れが正しく流れていない（逆に向いている）ためエントロピーが減少することを確認する。（図2.19）のように、全体で断熱された系の中に、高温熱源系（温度 $\varTheta_{\mathrm{H}}$ ）、低温熱源系（温度 $\varTheta_{\mathrm{L}}$ ）、低温から高温に熱 $Q$ を伝えるだけの反クラウジウスサイクルの系の三つの系がある熱力学第二法則クラウジウスの表現に反する場合である。ここでもエントロピーを先ほどのように $Q/\varTheta$ として計算をしてみよう。間のサイクルは同じ状態で動作するのでエントロピーは変化しない。高温熱源系は熱を受け取るので熱は正となり $\Delta S_{\mathrm{H}}=|Q|/\varTheta_{\mathrm{H}}$ となる。低温熱源系は熱を与えるので熱は負となり $\Delta S_{\mathrm{L}}=-|Q|/\varTheta_{\mathrm{L}}$ となる。高温熱源系でエントロピーは増加し、低温熱源系でエントロピーは減少する。全体での変化量 $\Delta S_{\mathrm{total}}$ は次のようになる。

	$\displaystyle\Delta S_{\mathrm{total}}$	$\displaystyle=\Delta S_{\mathrm{H}}+\Delta S_{\mathrm{cycle}}+\Delta S_{% \mathrm{L}}$
		$\displaystyle=\frac{\|Q\|}{\varTheta_{\mathrm{H}}}+0+\frac{-\|Q\|}{\varTheta_{% \mathrm{L}}}$
		$\displaystyle=\|Q\|\left(\frac{1}{\varTheta_{\mathrm{H}}}-\frac{1}{\varTheta_{% \mathrm{L}}}\right)<0$

温度は高温熱源系が低温熱源系よりも高い（ $\varTheta_{\mathrm{H}}>\varTheta_{\mathrm{L}}$ ）ため、全体でエントロピーは減少していることがわかる。熱力学第二法則に反する正しくない時間の向きでエントロピーが減少したので、エントロピーとして $Q/\varTheta$ を用いることはここの条件では目的にかなっている。

Figure 2.19: エントロピーと反クラウジウスサイクル

2.5.5 複数の熱源とサイクル（複数の系）

複数の熱源とサイクル（複数の系）が全体で断熱されている場合を考える。 $n$ 個の熱源でエントロピーを $Q/\varTheta$ と定義した場合に、次式のように全体でエントロピーが増大すると仮定する。

\displaystyle\sum^{n}_{i=1}\frac{Q_{i}}{\varTheta_{\mathrm{源i}}}\geq 0

(2.25)

上式が成り立つ場合に、n+1個の熱源でも次式のようにエントロピーが増大することを示す。

\sum^{n+1}_{i=1}\frac{Q_{i}}{\varTheta_{\mathrm{源i}}}\geq 0

このことが示せれば、一熱源（二つの系）、二熱源（三つの系）では成り立つことをすでに示しているから、エントロピーの増大が複数の熱源（複数の系）に対して一般的に成り立つと言える。

図2.20に示すように、n+1個の温度の異なる熱源と、その全ての複数熱源と熱交換をする複数熱源サイクルM、熱源nと熱源n+1の二つのみを熱源とする可逆サイクルRを考える。それぞれの熱源の温度は $\varTheta_{\mathrm{源1}}$ 、 $\varTheta_{\mathrm{源2}}$ 、 $\cdots$ 、 $\varTheta_{源n}$ 、 $\varTheta_{源n+1}$ 、サイクルMと熱源とで作用する熱を $Q_{\mathrm{M,1}}$ 、 $Q_{\mathrm{M,2}}$ 、 $\cdots$ 、 $Q_{\mathrm{M,}n}$ 、 $Q_{\mathrm{M,}n+1}$ 、可逆サイクルRが熱源 $n$ 、熱源 $n+1$ とやり取りする熱をそれぞれ $Q_{\mathrm{R,}n}$ 、 $Q_{\mathrm{R,}n+1}$ とする。熱源のエントロピー変化を考えるので、熱は熱源が受け取る向きを正とする。図2.20中でも熱が正となる向きを矢印の向きとしている。

Figure 2.20: 複数熱源

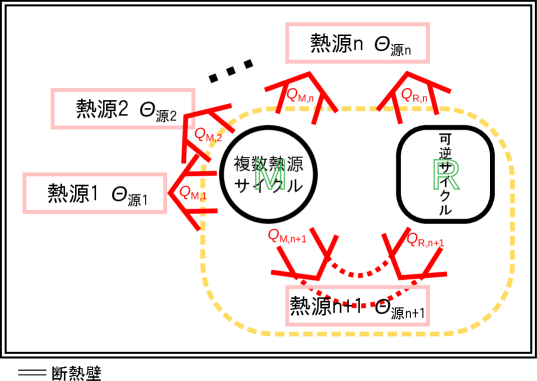
可逆サイクルRと複数熱源サイクルMは、熱源n+1と同じ大きさで違う向きの熱のやり取りをさせる。式で表すと次式となる²¹²¹21それぞれのサイクルの仕事の大きさが違う場合は、同じサイクルを複数個まとめて動作させて、それぞれの数を調整し、総計で同じ仕事となるように調整する。。

\displaystyle Q_{\mathrm{M,}n+1}+Q_{\mathrm{R,}n+1}=0

(2.26)

図2.20のオレンジの点線で囲った複数熱源サイクルM、熱源n+1、可逆サイクルRをまとめて一つのサイクルとして考えると、仮定の式(2.25)における $\dfrac{Q_{n}}{\varTheta_{n}}$ の項はサイクルMと可逆サイクルRでの熱の和で $\dfrac{Q_{\mathrm{M,}n}}{\varTheta_{n}}+\dfrac{Q_{\mathrm{R,}n}}{\varTheta_{n}}$ となるので、式(2.25)から次式が成り立つ。

\displaystyle\sum^{n-1}_{i=1}\frac{Q_{\mathrm{M,}i}}{\varTheta_{源i}}+\frac{Q_{% \mathrm{M,}n}}{\varTheta_{源n}}+\frac{Q_{\mathrm{R,}n}}{\varTheta_{源n}}\geq 0

(2.27)

可逆サイクルRは熱源 $n$ と熱源 $n+1$ の二つを熱源とするため式(2.16)が適用できる。

\displaystyle\frac{Q_{\mathrm{R,}n}}{\varTheta_{源n}}+\frac{Q_{\mathrm{R,}n+1}}% {\varTheta_{\mathrm{源}n+1}}=0

式(2.27)へ代入する。

\displaystyle\sum^{n-1}_{i=1}\frac{Q_{\mathrm{M,}i}}{\varTheta_{\mathrm{源}i}}+% \frac{Q_{\mathrm{M,}n}}{\varTheta_{\mathrm{源}n}}-\frac{Q_{\mathrm{R,}n+1}}{% \varTheta_{\mathrm{源}n+1}}\geq 0

式(2.26)により次式を得る。

	$\displaystyle\sum^{n-1}_{i=1}\frac{Q_{\mathrm{M,}i}}{\varTheta_{\mathrm{源}i}}+% \frac{Q_{\mathrm{M,}n}}{\varTheta_{\mathrm{源}n}}+\frac{Q_{\mathrm{M,}n+1}}{% \varTheta_{\mathrm{源}n+1}}\geq 0$
	$\displaystyle\sum^{n+1}_{i=1}\frac{Q_{\mathrm{M,}i}}{\varTheta_{\mathrm{源}i}}\geq 0$

これで、 $n$ 個の熱源で全体でエントロピーが増大するのであれば、 $n+1$ 個の複数熱源でも正しい時間の流れ（熱力学第二法則に反しない場合）ではエントロピーは増大することが確認できた。

2.5.6 無限個の熱源とサイクル（無限個の系）

無限個の熱源とサイクル（無限個の系）での全体のエントロピーの変化を考える。前節で複数の熱源でエントロピーが増大することが確認できた。複数熱源の数を限りなく無限個として、一つの熱源と極微少量の熱量 $\delta Q$ を交換すると、次式が成り立つ。

\displaystyle\sum^{\infty}_{i=1}\frac{\delta Q_{i}}{\varTheta_{\mathrm{源}i}}\geq 0

これは全体が断熱された中で、サイクルと熱のやり取りをしている一つの熱源の温度が変わる際にも適用できる。極微小な熱量 $\delta Q$ を受ける際の全ての系のサイクル一周分の熱源のエントロピー変化 $\Delta S_{\mathrm{total}}$ は次のように表すことができる²²²²22 $\oint$ は周回積分を表し、ここではサイクル一周分の積分である。。

\displaystyle\Delta S_{\mathrm{total}}=\oint\frac{\delta Q}{\varTheta_{\mathrm% {源}}}\geq 0

2.5.7 エントロピーの定義

エントロピーの定義として、変化量を熱量をその時の絶対温度で割った値とすると、複数の熱源においてはじめに示した条件を満たすことが示せた。しかし、ただ熱量でエントロピーを定義してしまうとエントロピーは状態量とならず、状態変化の過程が明らかな特別な状況でしか不可逆の指標として使えないため広く応用することができない。そこで、エントロピーの定義における熱 $Q$ を可逆過程の熱 $Q_{可}$ とするとエントロピーは状態量となり、ある特殊な状態が二つある場合にそれぞれに不可逆の度合いを計算することが出来るようになる。すなわち、どちらからどちらに時間が流れるのかがエントロピーを計算することで求めることが出来るようになり、応用の幅が大きく広がる。このことからエントロピーは可逆過程の熱をその時の絶対温度で割った値として次式(2.28)のように定義する。

\displaystyle\Delta S\equiv\frac{Q_{可}}{\varTheta}

(2.28)

上式からエントロピーの単位は[J/K]である。

また、極微小な可逆過程の熱量 $\mathrm{d}Q_{可}$ [J]により、次式のようにもエントロピーは定義できる ²³²³23通常の熱は状態により計算できないため $\delta Q$ で極微少量を表したが、可逆過程の熱は状態により決まる値で極微少な変化量として計算できるため $\mathrm{d}Q$ で表す。。

\displaystyle\mathrm{d}S\equiv\frac{\mathrm{d}Q_{可}}{\varTheta}

(2.29)

可逆過程の熱でエントロピーを定義したが、通常（不可逆過程）の熱のやり取りがあった場合にエントロピーが計算できなくなるわけではない。どのようにエントロピーを計算すれば良いかは付録B.8節 ${}^{\text{p.\ref{sec-RevIrevHeat}}}$ に考え方を示す。

2.5.8 問題

1.

断熱された閉じた系の中で温度 $\varTheta_{\mathrm{A}}$ [K]の物体Aから温度 $\varTheta_{\mathrm{B}}$ [K]の物体Bへ熱 $Q$ [J] $>$ 0が伝わるときの物体A、物体Bそれぞれと全体のエントロピーの変化量を求めよ。物体の温度は熱が伝わっても変化しないとする。

2.5.9 解答

1.

エントロピーの変化は式(2.28) ${}^{\text{p.\ref{eq-EntropyDelta}}}$ により表されるので熱が奪われる物体Aのエントロピー変化 $\Delta S_{\mathrm{A}}$ は次式で表される。

$\Delta S_{\mathrm{A}}=\dfrac{-Q}{\varTheta_{\mathrm{A}}}$

熱が与えられる物体Bでは次式となる。

$\Delta S_{\mathrm{B}}=\dfrac{Q}{\varTheta_{\mathrm{B}}}$

全体のエントロピーの変化 $\Delta S_{\mathrm{total}}$ は物体Aと物体Bの変化を足せばよいので次式となる。

$\Delta S_{\mathrm{total}}=\Delta S_{\mathrm{A}}+\Delta S_{\mathrm{B}}=\dfrac{-% Q}{\varTheta_{\mathrm{A}}}+\dfrac{Q}{\varTheta_{\mathrm{B}}}$

ここで、熱は温度の高い物体から低い物体に伝わるので $\varTheta_{\mathrm{A}}>\varTheta_{\mathrm{B}}$ となる。このことと上式より次の関係が成り立つ。

$\Delta S_{\mathrm{total}}=\dfrac{-Q}{\varTheta_{\mathrm{A}}}+\dfrac{Q}{% \varTheta_{\mathrm{B}}}>0$

以上のように、通常の熱が伝わる不可逆過程では全体のエントロピーは増加する。

2.4 可逆サイクル（可逆熱機関・可逆ヒートポンプ）の効率と熱力学的温度 References 2.6 ヘルムホルツの自由エネルギー

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。