


Next: 2.4.3 時間あたりに伝わる熱
Up: 2.4.2 対流によるエネルギーの出入
Previous: 2.4.2.8 圧縮性流体(密度 [kg/m ]は変化する)
対流により各面で時間当たりに出入する量は式(2.139)
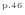 と各面の質量流量の式(2.27)-(2.32)
と各面の質量流量の式(2.27)-(2.32)
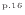 より次のように求まる。途中で相対する面の関係を式(2.11)
より次のように求まる。途中で相対する面の関係を式(2.11)
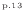 を用いて求める。
を用いて求める。
 軸に垂直
軸に垂直 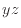 面左
面左-
 |
(2.149) |
 軸に垂直
軸に垂直 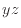 面右
面右-
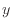 軸に垂直
軸に垂直 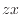 面下
面下-
 |
(2.151) |
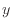 軸に垂直
軸に垂直 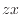 面上
面上-
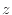 軸に垂直
軸に垂直 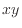 面後
面後-
 |
(2.153) |
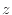 軸に垂直
軸に垂直 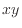 面前
面前-
上六式から、まずそれぞれの軸に沿った出入を求める。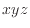 の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.22(2.1.6節
の各軸にそってコントロールボリュームから出て行く方向が負、入る方向が正になるように符号を加え、向かい合う面を足し合わせる2.22(2.1.6節
 )。
)。
 軸に沿った出入
軸に沿った出入- 式(2.150)
 式(2.151)
式(2.151)
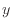 軸に沿った出入
軸に沿った出入- 式(2.152)
 式(2.153)
式(2.153)
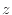 軸に沿った出入
軸に沿った出入- 式(2.154)
 式(2.155)
式(2.155)
xyz軸での出入の総和、式(2.156)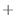 式(2.157)
式(2.157)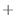 式(2.158)をとる。ここで、全ての項がコントロールボリュームの体積(
式(2.158)をとる。ここで、全ての項がコントロールボリュームの体積(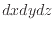 )で括られているため各境界面での区別はせず(2.1.7節
)で括られているため各境界面での区別はせず(2.1.7節
 )、下付きを外す。コントロールボリューム全体での対流による内部エネルギーの出入は次式で表される。
)、下付きを外す。コントロールボリューム全体での対流による内部エネルギーの出入は次式で表される。



Next: 2.4.3 時間あたりに伝わる熱
Up: 2.4.2 対流によるエネルギーの出入
Previous: 2.4.2.8 圧縮性流体(密度 [kg/m ]は変化する)
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。