5.1 閉じた系

閉じた系とは、周囲と物質の出入りがないが熱や仕事のやりとりはある系である¹¹1外部と物質の出入りがなく熱や仕事のやりとりもない系を“孤立系”という。外部と物質の出入りも熱や仕事のやりとりもある系を“開いた系”という。。系からの物質の出入りがないため、系内の質量は常に等しいが、体積は変化することもある。閉じた系のように一定の質量を考える系を検査質量とも呼ぶ。具体的な形状として、ピストンが閉じた系の例として挙げられることが多い。ここではこの閉じた系でのサイクルについて扱う。

5.1.1 平衡

平衡である状態のみを閉じた系では扱う。局所的な平衡は考えず、系全体が平衡である状況のみを考える。平衡とは無限の時間が経過した後の釣り合いがとれた状態であり、系の中が均一であり変化をしない状態である。ある平衡状態から異なる平衡状態へ変化する過程での途中の状態は扱わず、変化の前と平衡に達した後の状態を扱う。熱が伝わっている状態は必ず温度差があり非平衡であるため、熱が伝わっている状態は取り扱えず、伝わり終わった後の温度が均一な熱平衡になった状態を取り扱う。系の平衡には熱力学的平衡 (thermodynamic equilibrium) を考える ²²2熱力学的な取り扱いをする際、系の状態は熱力学的平衡が成り立っている必要がある。しかし、ある平衡状態から次の平衡状態へ変化する間の過程では必ずしも常に平衡状態が維持されている必要はない。変化中の非平衡の系を扱うことはできないが、変化前の平衡状態と変化後の平衡状態の系の変化については取り扱うことが出来る。。熱力学的平衡では以下の平衡がすべて成り立っていなくてはならない[1]。

熱平衡 (Thermal equilibrium): 系の内外で熱の移動がなく、さらに系内でも熱の移動がなく系内で温度が一定の状態
力学平衡 (Mechanical equilibrium): 系の内外で力が釣り合っており、さらに系内でも力が釣り合っていて系内で圧力が一定の状態
相平衡 (Phase equilibrium): 相の変化が釣り合っていて、それぞれの相の質量が変化せず一定の状態
化学的平衡 (Chemical equilibrium): 化学反応が釣り合っていて、それぞれの化学物質の質量が変化せず一定の状態

本章では熱力学的平衡にある閉じた系での変化を考える。

5.1.2 閉じた系の周囲とのやりとり

閉じた系の周囲とのやりとりとしては、物質の出入りがないため熱と仕事のみを考えれば良い。通常は周囲を壁に囲われた系である。

仕事のやりとりがある場合には、系を囲っている壁面の一部が必ず可動壁となる。この外と仕事のやりとりをする例として、図5.1のようにピストン形状の系を考える。ピストンの可動壁に壁を支える支持棒がついていると考え、系の圧力と釣り合うように支持棒に力を加える。仕事のやりとりのない過程では、固定して動かないようにする。通常系の外の空気などの流体によりピストンの外側には圧力が作用するが、ここでは考えやすくするため大気圧のような圧力はなく支持棒のみの力で支えられているとする ³³3 系外の流体の圧力が異なると支持棒の力が変わる。系が周囲にする仕事と、大気圧のような系外の流体に対する仕事と支持棒に対する仕事の和が等しくなるように、支持棒での仕事を変化させる。そのため、系外の流体の圧力の変化による系の周囲へする仕事への影響はない。指示棒と系外の流体にした仕事の和が系が周囲にした仕事である。ただし現実の熱機関では、取り出せる仕事は支持棒への仕事であり、系が周囲へした仕事から系外の流体（大気など）にした仕事の量だけ減少する。系の圧力と系外の流体の圧力、支持棒に加える力と仕事については付録D.1 ${}^{\text{p.\ref{sec-AppendixWork}}}$ に詳細を示す。。

Figure 5.1: 閉じた系と熱源

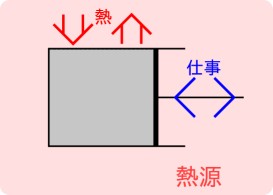
閉じた系での仕事は圧力と体積の変化から計算できる。ピストンが系にする仕事 $W$ [J]は力 $F$ [N]と移動距離 $\Delta x$ [m]で次式のように定義されている。

W=-F\Delta x

ここでは、系にされる仕事を正とし、系の体積が広がる方向にピストンが動く向きを正としているので、上式右辺に負号がついている。微少な移動距離 $\mathrm{d}x$ での微少な仕事 $\delta W$ ⁴⁴4 $\delta$ についてはA.1節 ${}^{\text{p.\ref{sec-WorkInexact}}}$ は次式となる。

\displaystyle\delta W=-F\mathrm{d}x

(5.1)

閉じた系ではピストンにかかる力 $F$ [N]は圧力 $P$ [Pa]とピストンの断面積 $A$ [m²]により

\displaystyle F=AP

(5.2)

と表される。また、ピストンを微小に動かした体積 $\mathrm{d}V$ [m³]は、ピストンの断面積 $A$ [m²]と、微小な移動距離（ピストンを動かした距離） $\mathrm{d}x$ [m]から、

\displaystyle\mathrm{d}V=A\mathrm{d}x

(5.3)

で表されるので、式(5.1)に式(5.2)と式(5.3)を順次代入し次式を得る。

	$\displaystyle\delta W$	$\displaystyle=-F\mathrm{d}x=-AP\mathrm{d}x$
		$\displaystyle=-P\mathrm{d}V$		(5.4)

となる。

周囲との熱のやりとりの際には、周囲を熱源と呼ぶ。熱源の状態を考える条件として、熱力学的平衡状態でなくてはならない（5.1.1節 ${}^{\text{p.\ref{sec-Equilibrium}}}$ ）ため、熱源はある一定の温度で一様な分布である必要がある。このため熱源の温度はすべて同じある一定の温度である⁵⁵5現実的な熱源は有限の大きさであるため熱のやり取りをすれば温度が変化するが、ここでは理想的な無限の大きさの熱源を考え、熱のやり取りをしても温度の変化は十分に小さく無視できるとする。。支持棒で可動壁を支えており系は熱源の圧力の影響を受けない。そのため、熱源で系に影響する条件は温度のみである。

5.1.3 サイクル

サイクルはこれまでにも出てきているが、ここで詳しく説明する。系がある状態1から何度か状態が変化し再度状態1へ戻る一連の過程をサイクルと呼ぶ。その一連の変化で高温物体から熱を奪い、低温物体へ熱を与え、周囲からされる仕事よりも周囲にする仕事が大きいサイクルを熱機関と呼ぶ。また、一連の変化で低温物体から熱を受け取り、高温物体へ熱を与え、周囲にする仕事よりも周囲からされる仕事が大きいサイクルをヒートポンプと呼ぶ。サイクルと周囲との熱や仕事のやりとりを考える際には、一連の過程での熱や仕事のやりとりの合計値を考える。サイクルの一連の過程では始めの状態に戻って終わるため始めと終わりの内部エネルギー $U$ [J]は等しく、サイクルの一連の過程での内部エネルギーの変化量 $\Delta U$ [J]は必ず次式のように0となる。

\displaystyle\Delta U=0

(5.5)

5.1.4 閉じた系のサイクルでの過程

閉じた系のサイクルでの過程のうち体積一定や圧力一定、温度一定、断熱のような特徴的な過程をいくつか示す。過程の始めと終わりは必ず熱力学的平衡であり、平衡ではない変化の途中は扱わない。系の温度を $T$ [℃またはK]、圧力を $P$ [Pa]、体積を $V$ [m³]、内部エネルギーを $U$ [J]、伝わった熱を $Q$ [J]、やりとりした仕事を $W$ [J]とする。また、過程の始めの系の状態に下付き「始」を終わりの状態に下付き「終」をつけて表す。熱力学第一法則の式(1.19) ${}^{\text{p.\ref{eq-1stLaw}}}$ から内部エネルギーの変化を知ることができる。

\displaystyle\Delta U=Q+W

(1.19)

等積過程

等積過程とは始めと終わりの体積が同じである過程である。想像しやすいのは、可動壁を固定し系の体積が変化しない（仕事のやりとりがない）状態で、周囲（熱源）と熱のみやりとりをする過程（図5.2）であろう。密閉された容器での変化は等積過程として扱える。この等積の過程で加熱される等積加熱では、周囲の温度が系より高い場合が考えられる。熱が伝わる過程は非平衡であるので、（系と熱源を離し、十分に時間が経った後）系内部が熱力学的平衡となってから過程を終了する ⁶⁶6過程の始めと終わりの状態は熱力学的平衡状態でなくてなはらない（5.1.1節 ${}^{\text{p.\ref{sec-Equilibrium}}}$ ）。。加えられた熱と同じ量だけ内部エネルギーが増加するため温度が上昇する。体積が一定で温度が上昇する過程では通常圧力も上昇する。

Figure 5.2: 等積過程

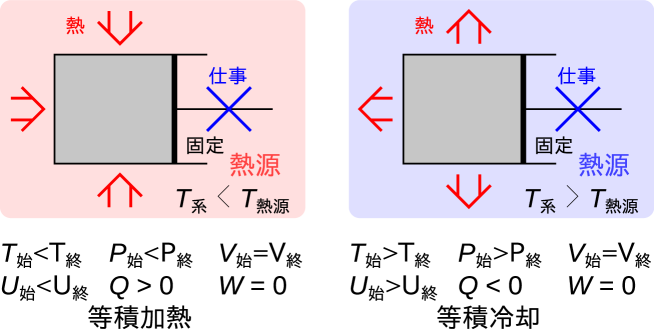
周囲の温度が系よりも低い場合には、系から周囲に熱が伝わり冷却される。冷却過程では、奪われた熱と同じ量だけ内部エネルギーが減少するため温度が下がる。体積が一定で温度が低下する過程では通常圧力も低下する。

閉じた系では始めと終わりの状態のみを考えるので、上に上げた変化以外にも過程中に体積が変化し、終わりの状態で始めと同じ体積の位置に戻る過程も考えられる。その際、摩擦などの影響で、系にされる仕事が系が周囲にする仕事よりも大きくなることがある。この仕事の差は摩擦などで発熱するので、体積が変化せず発熱だけした変化と捉えられる。

等圧過程

等圧過程とは始めと終わりの圧力が等しい過程であり、系と周囲で仕事と熱どちらもやりとりがある。系の内部を完全に常に同じ圧力に保ちながら変化をさせることは難しい。周囲から同じ圧力を加えていても、可動部かあれば摩擦で内部の圧力と加えた圧力が等しくならない。また、圧縮や膨張時に瞬間的に内部の圧力が変化するため一定の圧力にはならない。しかし、周囲からの圧力と内部の圧力は近い値となる。閉じた系では始めと終わりの状態のみを考えるので、等圧過程では変化中は一定圧力である必要はない。大気圧下での変化はだいたい等圧変化として扱える。

等圧過程の例として、周囲からかかる圧力が一定であり、温度の異なる熱源に接触している系を考える（図5.3）。等圧で膨張する場合には周囲に仕事をするため、同程度の熱を周囲から受け取るか、内部での発熱が必要である。周囲から熱を受け取る場合は、周囲の熱源の温度が系よりも高い。熱源から系に熱が伝わり系の温度が上昇し、圧力がわずかに周囲より高くなり膨張する。この場合では系は熱を受け仕事を周囲にする。圧力が一定で体積が増加するためには、一般的に温度は上昇しなくてはならない（気液二相の共存状態であれば温度は一定）。

Figure 5.3: 等圧過程

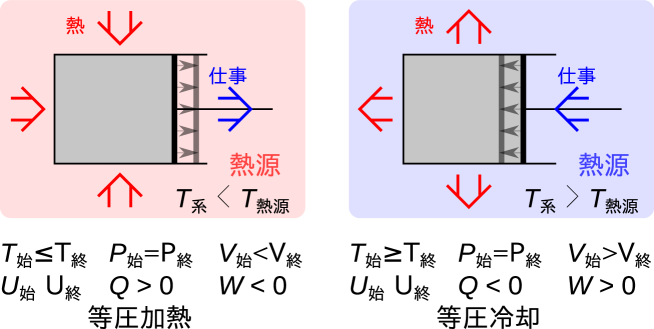
等圧での圧縮では周囲から仕事をされる。この過程を等圧で行うには、仕事と同程度の熱を周囲に伝えるか、内部で吸熱反応が必要である。周囲の熱源の温度が系よりも低い場合は、系から周囲に熱が伝わり系の温度が低下しわずかに周囲より圧力が低くなり収縮し、周囲から仕事をされることになる。この場合は周囲に熱を伝え系は仕事をされる。圧力が一定で体積が減少するためには、一般的に温度は低下しなくてはいけない（気液二相の共存状態であれば温度は一定）。

仕事と熱のエネルギーの向きが逆となるため、内部エネルギーの変化は系内部の物質の性質による。過程の終わりでは熱力学的平衡になってほしいので、過程が終わる前に系と熱源を離し系内部が熱力学的平衡となってから過程を終了する。

等温過程

等温過程とは始めと終わりが同じ温度となる過程で、系と周囲で仕事と熱のどちらもやりとりがある。2.3.2節 ${}^{\text{p.\ref{sec-Quasistatic}}}$ で出てきた準静等温過程も等温過程の一種である。通常の等温過程は始めと終わりが同じ温度であればよいが、準静等温過程は特殊で過程の全てで等温でなくてはならない。

等温過程の例として系の始めの温度と周囲（熱源）の温度が同じである条件での変化を考えよう（図5.4）。膨張して系が仕事をする過程では、系内部の圧力と釣り合う周囲からの圧力または力を小さくすると系が膨張する。系が膨張すると周囲に仕事をするので、内部エネルギーは低下し温度も低下する。系の温度が周囲温度より低くなるので周囲から系へ熱が伝わる⁷⁷7一様な温度をもつ一つの熱源から熱を取り出し仕事に変換しているが、系が膨張するという結果を残しているので熱力学第二法則トムソンの表現2.2.2節 ${}^{\text{p.\ref{sec-2ndLawThomson}}}$ には反しない。。同じ温度で体積が増加すると一般的に圧力は低下する（気液二相の共存状態であれば圧力は一定）。

Figure 5.4: 等温過程

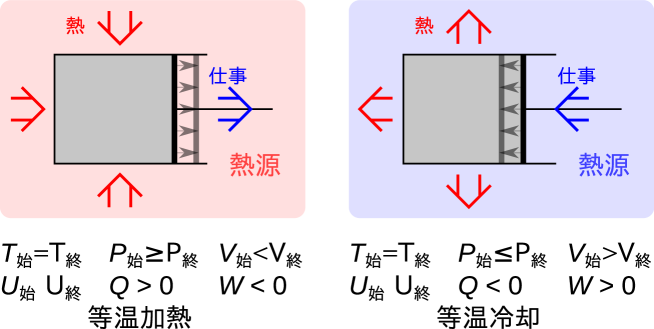
圧縮され系が仕事をされる過程では、系内部の圧力と釣り合う、周囲の圧力または力を大きくし圧縮が始まる。初めの状態から系が仕事をされ圧縮されると、内部エネルギーが増え温度が上昇する。系の温度が上昇し熱源よりも温度が高くなるため、熱が系から熱源へと伝わる。温度が一定で体積が減少すると一般的に圧力は上昇する（気液二相の共存状態であれば圧力は一定）。

仕事と熱のエネルギーの向きが逆となるため、内部エネルギーの変化は系内部の物質の性質による。系の圧縮や膨張（仕事の作用）が終わると熱源とやりとりがなくなる。その後、系と熱源が熱平衡となり系内部も熱力学的平衡となった後に過程を終了する。

等温過程において膨張で系がする仕事と圧縮で系がされる仕事の大きさは同じ変化でも不可逆性により変わる。不可逆性が大きいときは膨張時に得られる仕事が小さく、不可逆性がゼロの可逆変化である準静等温過程で最も大きくなる。圧縮に必要な仕事は不可逆性が大きいと大きくなり、可逆変化の準静等温過程で最も小さくなる（詳しくは付録B.6 ${}^{\text{p.\ref{sec-IsothermalProcess}}}$ ）。

断熱過程

断熱過程とは過程中に熱のやりとりがない過程である⁸⁸8始めと終わりの状態が決まっていればいいので、熱のやりとりがない過程と同じ状態で終わる過程、とも言える。。仕事のみ周囲とやりとりがある。

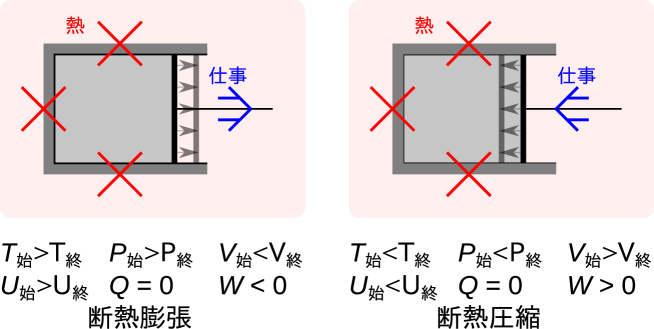
膨張過程では、図5.5に示すように、周囲に仕事をし、体積が増加する。周囲にした仕事と同量の内部エネルギーが減少し、温度が低下する。温度が低下し体積が増える過程では通常圧力は低下する。

圧縮過程では周囲から仕事をされ、体積が減少する。周囲から仕事をされた分、内部エネルギーが同量増加し、温度が上昇する。温度が上昇し体積が減る過程では通常圧力は上昇する。

Figure 5.5: 断熱過程

断熱過程において、発熱がなく不可逆性がゼロの、可逆になる過程が可逆断熱過程である。不可逆性が最も大きく仕事が全て発熱になってしまうのが自由膨張過程（付録D.2 ${}^{\text{p.\ref{sec-Expansion}}}$ ）である。

以上の過程を組み合わせることで、熱機関やヒートポンプのサイクルを構成することができる。

5.1.5 問題

問題として、どんな過程の組み合わせで、高温の熱源から低温の熱源へ伝わる熱から仕事を取り出したり（熱機関）、低温から高温へ熱を伝える（ヒートポンプ）ことができる、二つの熱源間で作動する閉じた系のサイクルとなるか考える。熱機関とヒートポンプのサイクルについては次節から具体的に示すが、理解を深めるために先に自分で考えてみよう。

次の必要な条件に合うように、これまで出てきた過程を組み合わせる。サイクル中で同じ過程を二回使ってもいい。

1.

サイクルとするために始めの状態と終わりの状態は同じ状態にする。
2.
熱機関では仕事を取り出すことが目的である。同時に、高温熱源から熱を受け取り、低温熱源へ熱を伝える。
1. (2-a)
  
  仕事を取り出す過程は必ず膨張する過程であるので、膨張過程を入れる。
2. (2-b)
  
  膨張後に増えた体積を元に戻すため、体積を戻す圧縮過程が必要である。
3. (2-c)
  
  仕事の作用する過程の和で仕事を外に取り出せなくてはならない。すなわち、膨張過程の仕事は圧縮過程の仕事よりも大きくなくてはならない。
4. (2-d)
  
  膨張過程の仕事を圧縮過程よりも大きくするために、高温熱源からの熱と低温熱源への熱を利用して、系の圧力を膨張過程で大きく、圧縮過程で小さくする。
3.
ヒートポンプでは低温熱源から熱を奪い、高温熱源へ熱を与えることが目的である。
1. (3-a)
  
  低温熱源から熱を奪う過程では、サイクルの温度は低温熱源より低くくなくてはならない。
2. (3-b)
  
  高温熱源へ熱を伝える過程では、サイクルの温度は高温熱源よりも高くなくてはならない。
3. (3-c)
  
  熱力学第二法則より系に仕事をする過程が必要である。
4. (3-d)
  
  系の温度は圧縮や膨張で圧力を変えることで変化する。

解答はこの後の「5.2 熱機関」と「5.3 ヒートポンプ」で見ていこう。

5 閉じた系のサイクル References 5.2 熱機関

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。