5.2 熱機関

熱機関について先程の問題の答えも含め詳しく見ていく。

5.2.1 熱機関の過程

熱機関の過程の例として熱と仕事のやりとりが分かりやすいように、一つの過程で熱か仕事どちらかだけのやりとりとなる等積過程と断熱過程で構成された、二つの熱源間で動作する閉じた系の熱機関を、5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ の条件2にそって考える。

（5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ 条件2-a）熱機関の目的は仕事を取り出すことであるので、仕事を取り出す膨張過程が必ず必要である。ここでは膨張過程として熱のやりとりがなく仕事のみやりとりする「断熱膨張過程」をサイクルに用いる。

（5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ 条件2-b）膨張した系を元の体積に戻さないとサイクルとして連続した動作ができないため、圧縮過程が必要である。ここでは圧縮過程には熱のやりとりがなく仕事のみやりとりする「断熱圧縮過程」を用いる。

（5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ の条件2-c）熱機関では全体として仕事を取り出すことが目的であるので、「断熱膨張過程」の仕事が「断熱圧縮過程」の仕事よりも大きくならなくてはならない。上記の「断熱膨張過程」と「断熱圧縮過程」は系から仕事を取り出す過程と仕事をする過程で、仕事の作用する向きは逆である。作用する仕事の大きさ $W$ は圧力 $P$ と体積変化量 $\Delta V$ により $W=P\Delta V$ で表されるので、体積変化量が同じであれば圧力が大きいほど仕事も大きくなる。すなわち「断熱膨張過程」の圧力を「断熱圧縮過程」の圧力よりも大きくしなくてはならない。そこで系の圧力を変えるために熱源との熱のやりとりを利用する。圧力を大きくするためには熱を加えれば温度が上昇し、圧力も大きくなる。また、熱を奪えば温度が下がり圧力が小さくなる。

（5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ 条件2-d）圧力を大きくしたい「断熱膨張過程」の前に熱を加えて、仕事を取り出した後に熱を奪い圧力を下げ「断熱圧縮過程」を行うことで、膨張で得られる仕事を圧縮で必要な仕事よりも大きくすることができる。ここでは熱を加える過程には「等積加熱過程」を、熱を奪う過程には「等積冷却過程」過程を用いる。

これまでの過程を順番に並べると次のようなサイクルとなる。

熱を奪って系の圧力を下げる「等積冷却過程」→低い圧力で仕事をして体積を元に戻す「断熱圧縮過程」→ 熱を加えて系の圧力を上げる「等積加熱過程」→高い圧力で仕事を取り出す「断熱膨張過程」→（始めから繰り返す）

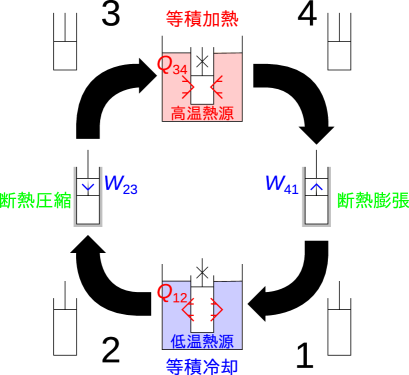
具体的な形を考えると、閉じた系として先を塞いだ注射器やピストンをイメージして、図5.6のようなサイクルとなる。

状態1からピストンを動かないように固定し、低温の熱源の中に入れる（例えば冷たい水の中）。ピストンから冷たい水に熱が伝わり、等積冷却過程でピストン内部の温度が下がり、圧力も下がる（状態2）。冷たい水からピストンを取り出し熱が伝わらないようにして、ピストンを押し断熱圧縮過程で体積を小さくする（状態3）。次はピストンを固定し温かいお湯の中にピストンを入れ等積加熱過程で変化させる。温度が上がり、圧力も上がる（状態4）。お湯からピストンを取り出し、元の状態に戻るまで断熱膨張過程でピストンを膨張させ仕事を取り出す（状態1）。元の状態に戻り一連の過程がサイクルとなる。

Figure 5.6: ピストンでの熱機関として動作するサイクル

5.2.2 圧力と体積の変化

圧力と体積の変化を、サイクルと周囲での仕事をやりとりに注目して見ていく。それぞれの過程では以下のことが起こっている。

: 1→2 （等積冷却過程）冷却され熱が周囲に伝わる → 内部の圧力が低下
: 2→3 （断熱圧縮過程）圧縮され周囲から仕事をされる → 体積が減少、圧力は上昇
: 3→4 （等積加熱過程）加熱され熱が周囲から伝わる → 内部の圧力が上昇
: 4→1 （断熱膨張過程）膨張し周囲に仕事をする → 体積が増加、圧力は低下

冷却（1→2）や加熱（3→4）をされると、圧力が変化し、断熱変化（2→3、4→1）で体積が変化することにより周囲と仕事のやりとりをする。圧力の変化の概略は図5.7のようになる。

Figure 5.7: 熱機関の圧力変化

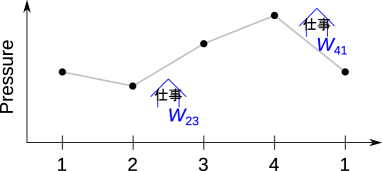
圧力と体積から、外部とやりとりする仕事が計算できるため、図5.7の圧力に加えて各過程の体積変化を同時に表示できると、仕事のやりとりが分かりやすく表示される。そこで縦軸に圧力 $P$ [Pa]、横軸に体積 $V$ [m³]を示した $P$ - $V$ 線図を図5.8に示す。

Figure 5.8: 熱機関の

P

V

線図

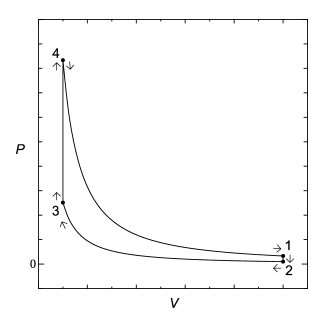
5.1.5問題 ${}^{\text{p.\ref{sec-questionHeatEnginePump}}}$ の条件2-cに示した熱機関として全体では仕事を取り出していることを $P$ - $V$ 線図（図5.8）を使って確認する。外部からサイクルに仕事をしている2→3の断熱圧縮過程での仕事 $W_{\mathrm{23}}$ [J]よりも、外部へサイクルが仕事をしている4→1の断熱膨張過程での仕事 $W_{\mathrm{41}}$ [J]が大きい必要がある。

式(5.4) ${}^{\text{p.\ref{eq-DifWork}}}$ より、仕事 $W$ [J]は圧力 $P$ [Pa]と微小体積変化 $\mathrm{d}V$ [m³]の積分により次式で表される。

	$\displaystyle W$	$\displaystyle=\int\delta W$
		$\displaystyle=-\int P\mathrm{d}V$		(5.6)

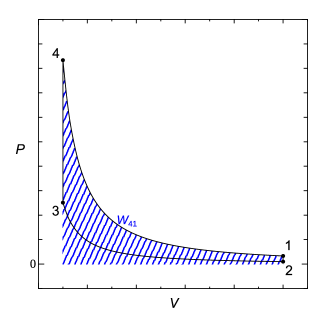
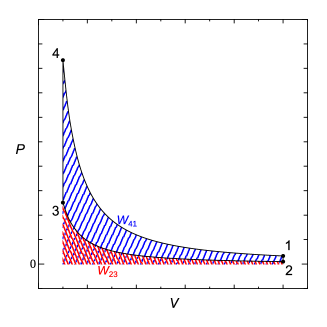
状態2から状態3への圧縮の変化での仕事を表す積分値は、 $P-V$ 線図で見ると図5.10で青斜線で表した面積となる。また、状態4から状態1への膨張の変化での仕事を表す積分値は図5.10で赤斜線で表した面積となる⁹⁹9状態2から状態3への圧縮の変化では積分の向きは負で、仕事の式5.6にマイナスがついてるから計算された仕事は正、系にされる仕事となる。状態4から状態1への膨張の変化では体積が増えて積分の向きは正、仕事の式5.6にマイナスがついているので計算された仕事は負、周囲にする仕事となる。。状態2から状態3と状態4から状態1での体積の変化量は同じであるので、どちらの仕事が大きいかは過程中の圧力によって決まる。図5.10から、状態2から状態3の平均圧力より、状態4から状態1の平均圧力が大きく、積分して得られる仕事も大きいことが一目で見て取れる。式で表すと次式で表される。

	$\displaystyle\left\|-\int^{3}_{2}P\mathrm{d}V\right\|$	$\displaystyle<\left\|-\int^{1}_{4}P\mathrm{d}V\right\|$
	$\displaystyle\|W_{\mathrm{23}}\|$	$\displaystyle<\|W_{\mathrm{41}}\|$

過程2→3では仕事 $W_{\mathrm{23}}$ をされるため正の値、過程4→1では仕事 $W_{\mathrm{41}}$ をするため負の値となることを考慮し、上式の絶対値記号を外すと次式が得られる。

\displaystyle W_{\mathrm{23}}<-W_{\mathrm{41}}

(5.7)

状態2から状態3では周囲から仕事をされ、状態4から状態1では周囲に仕事をしている。このサイクル全体では、図5.10の青斜線の面から赤斜線の面を引いた、ちょうどサイクルの線で囲まれた面積分の $|W_{\mathrm{41}}|-|W_{\mathrm{23}}|$ [J]の仕事を周囲にしている¹⁰¹⁰10絶対値を外すと $-W_{\mathrm{41}}-W_{\mathrm{23}}$ 。このように $P-V$ 線図のサイクルの面積として正味のサイクル全体が周囲にする仕事が求められる。

Figure 5.9: 熱機関の

P

V

線図と仕事１

Figure 5.10: 熱機関の

P

V

線図と仕事２

5.2.3 温度とエントロピーの変化

温度とエントロピーの変化を一緒に見ていく。温度の変化とエントロピーの変化量から外部とやりとりする熱を、式(2.29) ${}^{\text{p.\ref{eq-EntropyDefinitionD}}}$ を変形した次式より求めることができる ¹¹¹¹11元の式の $Q$ は可逆の熱だったが、不可逆で発生した熱を追加で熱源から受け取ったと考えることで、不可逆の過程も同じように扱うことができる。詳しくは付録B.8節 ${}^{\text{p.\ref{sec-RevIrevHeat}}}$ に考え方を示す。。

\displaystyle Q=\int\varTheta\mathrm{d}S

(5.8)

上式で $Q$ [J]はやりとりする熱、 $\varTheta$ [K]は絶対温度、 $S$ [J/K]はエントロピーである。温度とエントロピーを一緒に表す図を描けば、 $P$ - $V$ 線図で一目で仕事が分かったように、線図から熱を求めることができる。

それぞれの過程での温度とエントロピーの変化を見ていく。

: 1→2 （等積冷却過程）低温熱源に熱を渡しているので温度とエントロピーは低下する
: 2→3 （断熱圧縮過程）圧縮され圧力と温度が高くなる、エントロピーは断熱であるので変化しない（ここでは可逆断熱として考える。通常の不可逆断熱の場合はわずかにエントロピーが増加する。）
: 3→4 （等積加熱過程）高温熱源から熱を受け取っているので温度とエントロピーが増加する
: 4→1 （断熱膨張過程）膨張され圧力と温度が下がる、エントロピーは断熱であるので変化しない（ここでは可逆断熱として考える。通常の不可逆断熱の場合はわずかにエントロピーが増加する。）

このサイクルでの温度変化の概略を図5.11に示す。また、縦軸に温度 $T$ 、横軸にエントロピー $S$ をとった $T-S$ 線図を図5.12に示す。

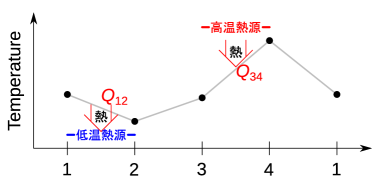
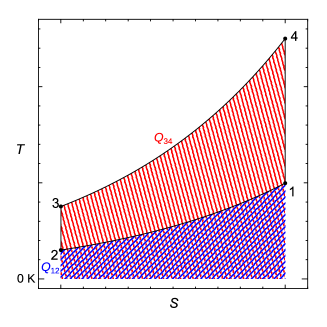
図5.11の温度変化の概略に示すように、周囲の温度は状態3から状態4の高温熱源が状態1から状態2の低温熱源よりも高い。このことから、このサイクルは高温熱源から熱を受け取り、低温熱源へ熱を与えている。

Figure 5.11: 熱機関の温度変化

Figure 5.12: 熱機関の

T

S

線図

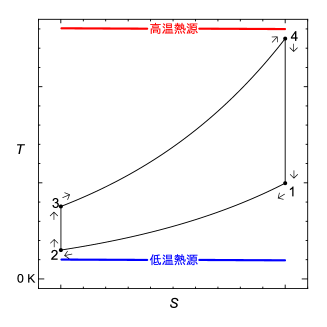
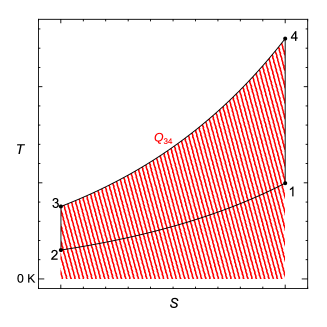
高温熱源からサイクルが熱を受け取る過程3→4での受け取る熱は、 $T-S$ 線図の3→4の区間を積分すれば計算することができる。熱と温度とエントロピーの関係式の式(5.8)での温度は絶対温度であるので図中では0 Kからの面積を積分で求める。過程3→4では積分は正の方向で、熱を求める式(5.8)から正の $T$ に対して熱も正となるので、求められる熱 $Q_{34}$ は正の値であり、サイクルが熱を受け取る方向である（図5.14の赤斜線の面）。

同様に低温熱源にサイクルが過程1→2で与える熱は、 $T-S$ 線図の1→2の区間を積分することで計算できる。ここでは積分の方向が負であるので、求められる熱 $Q_{12}$ は負の値であり、サイクルが熱を与える方向である（図5.14の青斜線の面）。図5.14の赤斜線と青斜線の差であるサイクル内の面積が、サイクル全体で伝わる熱量を表す。図5.14から明らかに過程3→4の温度が高く熱も大きいため、全体ではサイクルの面積だけサイクルが熱を受け取ることが分かる。

Figure 5.13: 熱機関の

T

S

線図と熱１

Figure 5.14: 熱機関の

T

S

線図と熱２

5.2.4 サイクル全体での仕事と熱

サイクル全体での仕事と熱の関係として、全体では熱から仕事に変換されていることを確認する。状態1から再度状態1へ戻るとき、内部エネルギーの値は等しく変化はゼロであるので、エネルギー保存の式(1.19) ${}^{\text{p.\ref{eq-1stLaw}}}$ から以下の式が成り立つ。

	$\displaystyle\Delta U$	$\displaystyle=Q_{\mathrm{12}}+W_{\mathrm{23}}+Q_{\mathrm{34}}+W_{\mathrm{41}}$
	$\displaystyle 0$	$\displaystyle=Q_{\mathrm{12}}+W_{\mathrm{23}}+Q_{\mathrm{34}}+W_{\mathrm{41}}$
	$\displaystyle W_{\mathrm{23}}+W_{\mathrm{41}}$	$\displaystyle=-Q_{\mathrm{12}}-Q_{\mathrm{34}}$

上式で表されるように、熱の差と、仕事の差は等しく ¹²¹²12左辺の仕事では二項とも正の符号がついているが $W_{23}$ は系に仕事をされているので正の値、 $W_{41}$ は系から周囲に仕事をしているので負の値となり、数値を入れると仕事の差となる。右辺の熱も同様である。、熱から仕事に変換されている。すなわち、図5.8のサイクル内の面積から求められるサイクル全体での仕事の大きさと、図5.12のサイクル内の面積から求められるサイクル全体での熱の大きさは等しい。

5.2.5 熱機関の表示

以上から、高温熱源から熱 $Q_{\mathrm{34}}$ [J]を受け取り、一部を仕事 $(|W_{\mathrm{41}}|-|W_{\mathrm{23}}|)$ [J]に変換し外部へ取り出し、高温熱源から受け取った熱より少ない残りの熱 $Q_{\mathrm{12}}$ [J]を低温熱源へ渡している、すなわち熱機関として動作していることがわかる。

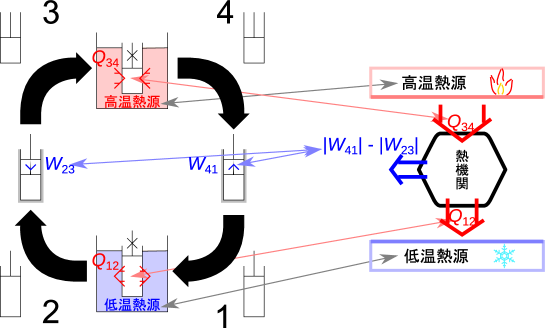
このように高温と低温の二つの熱源で動作する熱機関を1.5.1節以降では図5.15のように六角形状で表していた。仕事は周囲にした仕事と周囲からされた仕事の差 $(|W_{\mathrm{41}}|-|W_{\mathrm{23}}|)$ [J]をまとめて示した。図5.15では左の特定の四過程からなるサイクルと対応させているが、六角形状で表した際には熱機関であることだけを表しどのような過程で構成された熱機関でもよい。

Figure 5.15: 熱機関の表示

5.2.6 オットーサイクル

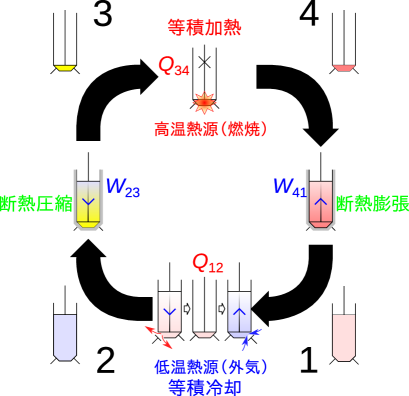
オットーサイクルと呼ばれるガソリンの理論サイクルが図5.6で例として示したサイクルである。このサイクルの各過程をガソリンエンジンと対応させると次のようになる（図5.16）。

: 1→2 （等積冷却過程）冷却され熱が周囲に伝わる → 燃焼後のガソリンと空気の混合気体を捨てて新しい空気を取り込む。排気して吸気をするとピストンが同じ位置に戻るので、これで等積の一過程とする
: 2→3 （断熱圧縮過程）圧縮され周囲から仕事をされる → 他のピストンから仕事をされ空気が圧縮される
: 3→4 （等積加熱過程）加熱され熱が周囲から伝わる → ガソリンと空気の混合気体に点火し瞬間的に燃焼させる。燃焼時間は一瞬であるため膨張による体積変化はほとんどなく、燃焼熱により加熱されるので、等積加熱となる
: 4→1 （断熱膨張過程）膨張し周囲に仕事をする → 前過程で圧力が上がっているので、膨張することで周囲に仕事をする

ガソリンエンジンでは作動流体が熱源となる。低温側では低温熱源となる大気を直接サイクルに取り込み、高温側では作動流体を直接燃焼させることで高温熱源とする。作動流体が熱源となるので、熱源と作動流体で熱交換をする必要がない¹³¹³13他の熱交換をするサイクルの場合は、熱源と作動流体で熱交換をする際に必ず温度差が必要となるため、高温側で作動流体の温度は高温熱源より低く、低温側では低温熱源よりも高くなり、作動流体での高温と低温の温度差が小さくなる。。ガソリンエンジンのように作動流体が熱源となるサイクルでは熱交換により作動流体の温度差が小さくなることがないためサイクルの効率が高くなる。効率は30-40％程度である[12][26][9]。

Figure 5.16: オットーサイクル

エンジンの他に実際に世の中で使われている熱機関として閉じた系のサイクルではないが火力発電所や原子力発電所がある。発電所の蒸気タービンを用いた汽力発電は系の中の物質に水を用いている。発電所と図5.6 ${}^{\text{p.\ref{fig-ClosedCycleVolumeHeatengine}}}$ のサイクルの対応は以下のようになっている。

: 1→2 冷却され熱が周囲に伝わる : 復水器（海水で冷却）
: 2→3 圧縮され周囲から仕事をされる : ポンプ（水を循環させる）
: 3→4 加熱され熱が周囲から伝わる : ボイラー（燃焼や核反応で水を沸騰させる）
: 4→1 膨張し周囲に仕事をする : 蒸気タービン（発電機へとつながっており電気を発生させる）

新しい火力発電所では、エンジンと同じく作動流体を直接熱源とするガスタービンと蒸気タービンを併用したコンバインドサイクルを用いて50～60％と高効率な発電をしている[25]。

5.1 閉じた系 References 5.3 ヒートポンプ

この図を含む文章の著作権は椿耕太郎にあり、クリエイティブ・コモンズ表示 - 非営利 - 改変禁止 4.0 国際ライセンスの下に公開する。最新版およびpdf版はhttps://camelllia.netで公開している。htmlファイルは LaTeXML

を用いて作成した。

	$\displaystyle\left\|-\int^{3}_{2}P\mathrm{d}V\right\|$	$\displaystyle<\left\|-\int^{1}_{4}P\mathrm{d}V\right\|$
	$\displaystyle\|W_{\mathrm{23}}\|$	$\displaystyle<\|W_{\mathrm{41}}\|$