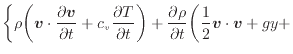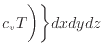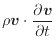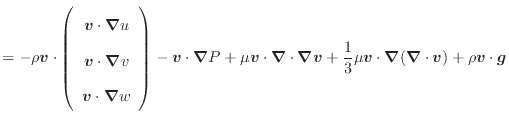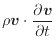


Next: 2.4.5.2 非圧縮性流体(密度 [kg/m ]は一定)
Up: 2.4.5 エネルギー保存式
Previous: 2.4.5 エネルギー保存式
式(2.94)
 へ、式(2.95)
へ、式(2.95)
 、式(2.107)
、式(2.107)
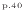 、式(2.128)
、式(2.128)
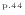 、式(2.149)
、式(2.149)
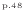 、式(2.170)
、式(2.170)
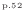 、式(2.182)
、式(2.182)
 を入れると次式が導かれる(エネルギー散逸関数
を入れると次式が導かれる(エネルギー散逸関数 は十分に小さいと考え無視する)。
は十分に小さいと考え無視する)。
dxdydzで両辺を割り括弧を外すと次式となる。
ここで質量保存式の式(2.37)
 より、
より、
これを上式(2.185)
 の左辺に代入し整理すると次式となる。
の左辺に代入し整理すると次式となる。
上式から運動量の保存式(2.90)
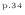 と速度ベクトル
と速度ベクトル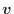 [m/s]の内積を引く。式(2.90)
[m/s]の内積を引く。式(2.90)
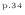 と
と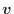 [m/s]の内積は以下のようになる(両辺に
[m/s]の内積は以下のようになる(両辺に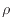 [kg/m
[kg/m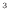 ]を掛けている)。
]を掛けている)。
上式を式(A.9)
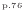 の変形と
の変形と
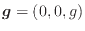 [m/s
[m/s ]の計算をすると次式となる。
]の計算をすると次式となる。
式(2.186)
 から上式を引くと次式のエネルギー保存式を得る。
から上式を引くと次式のエネルギー保存式を得る。



Next: 2.4.5.2 非圧縮性流体(密度 [kg/m ]は一定)
Up: 2.4.5 エネルギー保存式
Previous: 2.4.5 エネルギー保存式
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() へ、式(2.95)
へ、式(2.95)
![]() 、式(2.107)
、式(2.107)
![]() 、式(2.128)
、式(2.128)
![]() 、式(2.149)
、式(2.149)
![]() 、式(2.170)
、式(2.170)
![]() 、式(2.182)
、式(2.182)
![]() を入れると次式が導かれる(エネルギー散逸関数
を入れると次式が導かれる(エネルギー散逸関数![]() は十分に小さいと考え無視する)。
は十分に小さいと考え無視する)。