


Next: 2.4.1 持っている全エネルギーの時間変化
Up: 2. 私でも分かる! 支配方程式
Previous: 2.3.5.2 非圧縮性流体(密度 [kg/m ]は一定)
保存の対象として以下のエネルギーを考える。
- 運動エネルギー(運動している物体が持っているエネルギー)
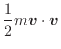
- 位置エネルギー(重力によるエネルギー)
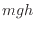
- 界面エネルギー(界面を持つ流体間でのエネルギー ここでは考慮しない)
- 内部エネルギー(系の持っているエネルギーから、運動・位置・界面エネルギーを除いたもの。主に顕熱
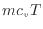 と潜熱であるが、ここでは顕熱のみを考慮する。)
と潜熱であるが、ここでは顕熱のみを考慮する。)
ここで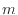 [kg]は保存対象の質量、
[kg]は保存対象の質量、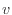 [m/s]は速度、
[m/s]は速度、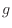 [m/s
[m/s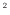 ]は重力加速度、
]は重力加速度、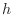 [m]は基準からの高さ、
[m]は基準からの高さ、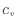 [J/(K
[J/(K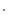 kg)]は定積比熱、
kg)]は定積比熱、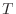 [K]は温度である。
[K]は温度である。
エネルギーの保存式は閉じた系では内部エネルギー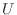 [J]のみを考慮し熱力学の第一法則より次式となる。
[J]のみを考慮し熱力学の第一法則より次式となる。
ここで、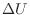 [J]は系の保有する内部エネルギーの変化量、
[J]は系の保有する内部エネルギーの変化量、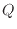 [J]は熱、
[J]は熱、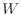 [J]は仕事である。この系の内部エネルギーの時間変化量は、時間あたりに伝わる熱
[J]は仕事である。この系の内部エネルギーの時間変化量は、時間あたりに伝わる熱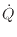 [W]と時間あたりの仕事
[W]と時間あたりの仕事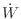 [W]で次のように表される。
[W]で次のように表される。
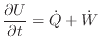 |
(2.92) |
今は開いた系(流れ系)を考えているので、上式(2.93)
 の左辺の全エネルギー(運動・位置・内部エネルギー)の時間変化と右辺の“時間あたりに伝わる熱”、“時間あたりの仕事”に右辺の対流により運ばれる運動・位置・内部エネルギーが加えられる。“時間あたりに伝わる熱”と“時間あたりの仕事”が式(2.4)
の左辺の全エネルギー(運動・位置・内部エネルギー)の時間変化と右辺の“時間あたりに伝わる熱”、“時間あたりの仕事”に右辺の対流により運ばれる運動・位置・内部エネルギーが加えられる。“時間あたりに伝わる熱”と“時間あたりの仕事”が式(2.4)
 における“境界面での作用による出入量”に、“生成エネルギー”が“体積に対する変化量”に対応する。このことから、エネルギー方程式は次のように書ける。
における“境界面での作用による出入量”に、“生成エネルギー”が“体積に対する変化量”に対応する。このことから、エネルギー方程式は次のように書ける。
式(2.94)
 の各項について考えていく。その際、生成エネルギーは考慮しない。
の各項について考えていく。その際、生成エネルギーは考慮しない。
Subsections



Next: 2.4.1 持っている全エネルギーの時間変化
Up: 2. 私でも分かる! 支配方程式
Previous: 2.3.5.2 非圧縮性流体(密度 [kg/m ]は一定)
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() [J]のみを考慮し熱力学の第一法則より次式となる。
[J]のみを考慮し熱力学の第一法則より次式となる。
![]() の左辺の全エネルギー(運動・位置・内部エネルギー)の時間変化と右辺の“時間あたりに伝わる熱”、“時間あたりの仕事”に右辺の対流により運ばれる運動・位置・内部エネルギーが加えられる。“時間あたりに伝わる熱”と“時間あたりの仕事”が式(2.4)
の左辺の全エネルギー(運動・位置・内部エネルギー)の時間変化と右辺の“時間あたりに伝わる熱”、“時間あたりの仕事”に右辺の対流により運ばれる運動・位置・内部エネルギーが加えられる。“時間あたりに伝わる熱”と“時間あたりの仕事”が式(2.4)
![]() における“境界面での作用による出入量”に、“生成エネルギー”が“体積に対する変化量”に対応する。このことから、エネルギー方程式は次のように書ける。
における“境界面での作用による出入量”に、“生成エネルギー”が“体積に対する変化量”に対応する。このことから、エネルギー方程式は次のように書ける。